Hostname: page-component-8448b6f56d-m8qmq Total loading time: 0 Render date: 2024-04-23T07:33:40.634Z Has data issue: false hasContentIssue false
  • English
  • Français

Index type invariants for twisted signature complexes and homotopy invariance

Published online by Cambridge University Press:  24 February 2014

MOULAY TAHAR BENAMEUR  and
VARGHESE MATHAI
MOULAY TAHAR BENAMEUR
Affiliation:
Institut de Mathématiques et Modélisation de Montpellier, UMR 5149, Université Montpellier 2, Case 051, 34095, Montpellier Cedex 5, France. e-mail: moulay.benameur@univ-montp2.fr
VARGHESE MATHAI
Affiliation:
Department of Mathematics, University of Adelaide, Adelaide 5005, Australia. e-mail: mathai.varghese@adelaide.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

For a closed, oriented, odd dimensional manifold X, we define the rho invariant ρ(X,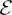${\cal E}$,H) for the twisted odd signature operator valued in a flat hermitian vector bundle 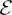${\cal E}$, where H = ∑ ij+1H2j+1 is an odd-degree closed differential form on X and H2j+1 is a real-valued differential form of degree 2j+1. We show that ρ(X,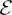${\cal E}$,H) is independent of the choice of metrics on X and 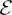${\cal E}$ and of the representative H in the cohomology class [H]. We establish some basic functorial properties of the twisted rho invariant. We express the twisted eta invariant in terms of spectral flow and the usual eta invariant. In particular, we get a simple expression for it on closed oriented 3-dimensional manifolds with a degree three flux form. A core technique used is our analogue of the Atiyah–Patodi–Singer theorem, which we establish for the twisted signature operator on a compact, oriented manifold with boundary. The homotopy invariance of the rho invariant ρ(X,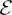${\cal E}$,H) is more delicate to establish, and is settled under further hypotheses on the fundamental group of X.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 156 , Issue 3 , May 2014 , pp. 473 - 503
Copyright
Copyright © Cambridge Philosophical Society 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Atiyah, M. F., Patodi, V. K. and Singer, I. M.Spectral asymmetry and Riemannian geometry, I. Math. Proc. Camb. Phil. Soc. 77 (1975), 43–69, MR0397797, Zbl 0297.58008.Google Scholar
[2]Atiyah, M. F., Patodi, V. K. and Singer, I. M.Spectral asymmetry and Riemannian geometry, II. Math. Proc. Camb. Phil. Soc. 78 (1975), no. 3, 405–432, MR0397798, Zbl 0314.58016.Google Scholar
[3]Atiyah, M. F., Patodi, V. K. and Singer, I. M.Spectral asymmetry and Riemannian geometry, III. Math. Proc. Camb. Phil. Soc. 79 (1976), no. 1, 71–99, MR0397799, Zbl 0325.58015.CrossRefGoogle Scholar
[4]Atiyah, M. F. and Singer, I. M.The index of elliptic operators, III. Ann. of Math. 87 (1968), 546–604, MR0236952.Google Scholar
[5]Atiyah, M. F. and Segal, G.Twisted K-theory and cohomology, in: Griffith, P.A. (Ed.), Inspired by S.S. Chern, Nankai Tracts Math., vol. 11 (World Scientific Publishing, Hackensack, NJ, 2006), pp. 5–43, [arXiv:math.AT/0510674], MR2307274, Zbl 1138.19003.CrossRefGoogle Scholar
[6]Baum, P. and Connes, A.Chern Character for Discrete Groups. A Fte of Topology, 163232 (Academic Press, Boston, MA, 1988), MR0928402.Google Scholar
[7]Benameur, M. T. and Heitsch, J.The twisted higher harmonic signature for foliations. J. Differential Geom. 87 (2011), no. 3, 389–467 [arXiv:0711.0352] MR2819544.CrossRefGoogle Scholar
[8]Benameur, M. T. and Mathai, V.Conformal invariants of twisted Dirac operators and positive scalar curvature. J. Geometry and Physics 70 (2013), 39–47 [arXiv:1210.0301], MR3054283.Google Scholar
[9]Benameur, M. T. and Mathai, V.Spectral sections, twisted rho invariants and positive scalar curvature, 25 pages [arXiv:1309.5746].Google Scholar
[10]Benameur, M. T. and Piazza, P.Index, eta and rho invariants on foliated bundles. Astérisque 327 (2009), 201–287, MR2642361.Google Scholar
[11]Benameur, M. T. and Roy, I.Leafwise homotopies and Hilbert-Poincare complexes. I. Regular HP-complexes and leafwise pull-back maps [arXiv:1109.0263].Google Scholar
[12]Berline, N., Getzler, E. and Vergne, M.Heat Kernels and Dirac operators. Grund. Math. Wissen. 298 (Springer-Verlag, Berlin, 1992), MR1215720, Zbl 0744.58001.CrossRefGoogle Scholar
[13]Bismut, J.-M.A local index theorem for non-Kähler manifolds. Math. Ann. 284 (1989), no. 4, 681–699, MR1006380.CrossRefGoogle Scholar
[14]Bismut, J-M. and Freed, D. S.The analysis of elliptic families. I. Metrics and connections on determinant bundles. Comm. Math. Phys. 106 (1986), no. 1, 159–176, MR0853982.Google Scholar
[15]Bott, R. and Tu, L.Differential forms in algebraic topology. Grad. Texts Math. vol. 82 (Springer-Verlag, New York-Berlin, 1982), MR0658304, Zbl 0496.55001.Google Scholar
[16]Bouwknegt, P., Carey, A., Mathai, V., Murray, M. and Stevenson, D.Twisted K-theory and K-theory of bundle gerbes. Commun. Math. Phys. 228 (2002), 17–49 [arXiv:hep-th/0106194], MR1911247, Zbl 1036.19005.CrossRefGoogle Scholar
[17]Bouwknegt, P., Evslin, J. and Mathai, V.T-duality: topology change from H-flux. Commun. Math. Phys. 249 (2004), 383–415 [arXiv:hep-th/0306062], MR2080959, Zbl 1062.81119.CrossRefGoogle Scholar
[18]Brüning, J. and Sunada, T.On the spectrum of periodic elliptic operators. Nagoya Math. J. 126 (1992), 159–171, MR1171598.Google Scholar
[19]Cardona, A., Ducourtioux, C. and Paycha, S.From tracial anomalies to anomalies in quantum field theory. Commun. Math. Phys. 242 (2003), no. 1–2, 315, MR2018268.CrossRefGoogle Scholar
[20]Cherix, P.–A., Cowling, M., Jolissaint, P., Julg, P. and Valette, A.Groups with the Haagerup property. Gromov's a-T-menability. Progr. Math. 197 (Birkhäuser Verlag, Basel, 2001), MR1852148.Google Scholar
[21]de Rham, G.Differentiable Manifolds. Forms, Currents, Harmonic Forms. Grund. Math. Wissen. 266 (Springer-Verlag, Berlin, 1984), x+167, pp MR0760450.Google Scholar
[22]Dodziuk, J. and Mathai, V.Approximating L 2 invariants of amenable covering spaces: A heat kernel approach. Contemp. Math. 211 (1997), 151–167, MR1476985.Google Scholar
[23]Gates, S. J., Hull, C. M. and Rocek, M.Twisted multiplets and new supersymmetric nonlinear sigma models. Nuclear Phys. B 248 (1984), 157, MR0776369.CrossRefGoogle Scholar
[24]Getzler, E.The odd Chern character in cyclic homology and spectral flow. Topology 32 (1993), no. 3, 489–507, MR1231957.Google Scholar
[25]Gilkey, P. B.Invariance Theory, the Heat Equation, and the Atiyah–Singer Index Theorem. Math. Lecture Series, vol. 11 (Publish or Perish, Inc., Wilmington, DE, 1984), MR0783634, Zbl 0565.58035; 2nd ed. (Studies Adv. Math.), (CRC Press, Boca Raton, FL, 1995), MR1396308, Zbl 0856.58001.Google Scholar
[26]Gualtieri, M. Generalized complex geometry. Ph.D thesis, Oxford University (2003), [arXiv:math/0401221].Google Scholar
[27]Higson, N. and Roe, J.K-homology, assembly and rigidity theorems for relative eta invariants. Pure Appl. Math. Q. 6 (2010), no. 2, Special Issue: in honor of Michael Atiyah and Isadore Singer, 555–601, MR2761858.Google Scholar
[28]Higson, N. and Roe, J.Mapping surgery to analysis. I. Analytic signatures. K-Theory 33 (2005), no. 4, 277–299, MR2220522.Google Scholar
[29]Higson, N. and Roe, J.Mapping surgery to analysis. II. Analytic signatures. Geometric signatures. K-Theory 33 (2005), no. 4, 301–324, MR2220523.Google Scholar
[30]Hitchin, N.Generalized Calabi-Yau manifolds. Quart. J. Math. 54 (2003), 281–308, [arXiv:math/0209099], MR2013140, Zbl 1076.32019.Google Scholar
[K]Kac, M.Can one hear the shape of a drum? Amer. Math. Monthly 73 (1966), 1–23, MR0201237.Google Scholar
[31]Keswani, N.Relative eta-invariants and C*-algebra K-theory. Topology 39 (2000), no. 5, 957–983, MR1763959.Google Scholar
[32]Kostant, B.A cubic Dirac operator and the emergence of Euler number multiplets of representations for equal rank subgroups. Duke Math. J. 100 (1999), no. 3, 447–501, MR1719734.CrossRefGoogle Scholar
[33]Lance, E. C.Hilbert C*-Modules. A Toolkit for Operator Algebraists. London Mathematical Society Lecture Note Series, 210. (Cambridge University Press, Cambridge, 1995), x+130 pp, MR1325694.Google Scholar
[34]Landweber, G. Dirac operators on loop spaces. Ph.D. thesis, Harvard University (1999).Google Scholar
[35]Mathai, V. and Wu, S.Analytic torsion for twisted de Rham complexes. J. Differential Geom. 88 no. 2 (2011), 297–332 [arXiv:math/0810.4204], MR2838268.Google Scholar
[36]Mathai, V. and Wu, S.Twisted analytic torsion. Sci. China Math. 53 (2010), no. 3, 555–563, [arXiv:math/0912.2184], MR2608312, Zbl 1202.58019.CrossRefGoogle Scholar
[37]Mathai, V. and Wu, S. Analytic torsion of ${\mathbb Z}_2$-graded elliptic complexes. Contemp. Math. 546 (2011), 199–212, MR2815136.Google Scholar
[38]Milnor, J.A note on curvature and fundamental group. J. Diff. Geom. 2 (1968), 1–7, MR0232311.Google Scholar
[39]Ray, D. B. and Singer, I. M.R-torsion and the Laplacian on Riemannian manifolds. Adv. Math. 7 (1971), 145–210, MR0295381, Zbl 0239.58014.Google Scholar
[40]Rohm, R. and Witten, E.The antisymmetric tensor field in superstring theory. Ann. Phys. 170 (1986), 454–489, MR0851628.Google Scholar
[41]Schwarz, G.Hodge decomposition method for solving boundary value problems. Lecture Notes in Mathematics, 1607 (Springer-Verlag, Berlin, 1995), MR1367287.Google Scholar
[42]Slebarski, S.Dirac operators on a compact Lie group. Bull. London Math. Soc. 17 (1985), no. 6, 579–583, MR0813743.Google Scholar
[43]Strominger, A.Superstrings with torsion. Nuclear Phys. B 274 (1986), 253–284, MR0851702.CrossRefGoogle Scholar
[44]Van, P.Nieuwenhuizen. Supergravity. Phys. Rep. 68 (1981), 189–398, MR0615178.Google Scholar