Hostname: page-component-76fb5796d-wq484 Total loading time: 0 Render date: 2024-04-25T12:29:15.946Z Has data issue: false hasContentIssue false
  • English
  • Français

Inverse spectral problems for compact Hankel operators

Part of: Special classes of linear operators Infinite-dimensional Hamiltonian systems

Published online by Cambridge University Press:  18 April 2013

Patrick Gérard  and
Sandrine Grellier
Patrick Gérard
Affiliation:
Université Paris-Sud XI, Laboratoire de Mathématiques d’Orsay, CNRS, UMR 8628, France Institut Universitaire de France, France (Patrick.Gerard@math.u-psud.fr)
Sandrine Grellier
Affiliation:
Fédération Denis Poisson, MAPMO-UMR 6628, Département de Mathématiques, Université d’Orleans, 45067 Orléans Cedex 2, France (Sandrine.Grellier@univ-orleans.fr)
Get access Rights & Permissions [Opens in a new window]

Abstract

Given two arbitrary sequences 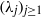$({\lambda }_{j} )_{j\geq 1} $ and 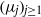$({\mu }_{j} )_{j\geq 1} $ of real numbers satisfying

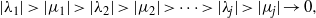$$\begin{eqnarray*}\displaystyle \vert {\lambda }_{1} \vert \gt \vert {\mu }_{1} \vert \gt \vert {\lambda }_{2} \vert \gt \vert {\mu }_{2} \vert \gt \cdots \gt \vert {\lambda }_{j} \vert \gt \vert {\mu }_{j} \vert \rightarrow 0, &&\displaystyle\end{eqnarray*}$$
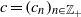we prove that there exists a unique sequence $c= ({c}_{n} )_{n\in { \mathbb{Z} }_{+ } } $, real valued, such that the Hankel operators 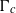${\Gamma }_{c} $ and 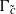${\Gamma }_{\tilde {c} } $ of symbols 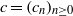$c= ({c}_{n} )_{n\geq 0} $ and 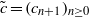$\tilde {c} = ({c}_{n+ 1} )_{n\geq 0} $, respectively, are selfadjoint compact operators on 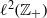${\ell }^{2} ({ \mathbb{Z} }_{+ } )$ and have the sequences 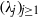$({\lambda }_{j} )_{j\geq 1} $ and 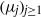$({\mu }_{j} )_{j\geq 1} $, respectively, as non-zero eigenvalues. Moreover, we give an explicit formula for $c$ and we describe the kernel of 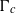${\Gamma }_{c} $ and of 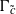${\Gamma }_{\tilde {c} } $ in terms of the sequences 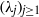$({\lambda }_{j} )_{j\geq 1} $ and 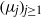$({\mu }_{j} )_{j\geq 1} $. More generally, given two arbitrary sequences 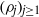$({\rho }_{j} )_{j\geq 1} $ and 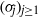$({\sigma }_{j} )_{j\geq 1} $ of positive numbers satisfying
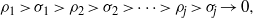$$\begin{eqnarray*}\displaystyle {\rho }_{1} \gt {\sigma }_{1} \gt {\rho }_{2} \gt {\sigma }_{2} \gt \cdots \gt {\rho }_{j} \gt {\sigma }_{j} \rightarrow 0, &&\displaystyle\end{eqnarray*}$$
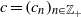 we describe the set of sequences $c= ({c}_{n} )_{n\in { \mathbb{Z} }_{+ } } $ of complex numbers such that the Hankel operators 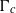${\Gamma }_{c} $ and 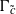${\Gamma }_{\tilde {c} } $ are compact on 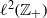${\ell }^{2} ({ \mathbb{Z} }_{+ } )$ and have sequences 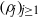$({\rho }_{j} )_{j\geq 1} $ and 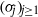$({\sigma }_{j} )_{j\geq 1} $, respectively, as non-zero singular values.

Keywords

Hankel operatorsinverse spectral problemscompressed shift operatoraction–angle variables

MSC classification

Secondary: 47B35: Toeplitz operators, Hankel operators, Wiener-Hopf operators 37K15: Integration of completely integrable systems by inverse spectral and scattering methods
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 13 , Issue 2 , April 2014 , pp. 273 - 301
Copyright
©Cambridge University Press 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adamyan, V. M., Arov, D. Z. and Krein, M. G., Analytic properties of the Schmidt pairs of a Hankel operator and the generalized Schur–Takagi problem, Mat. Sb. (N.S.) 86 (128) (1971), 34–75 (in Russian).Google Scholar
Gérard, P. and Grellier, S., The cubic Szegő equation, Ann. Sci. Éc. Norm. Supér 43 (2010), 761–810.Google Scholar
Gérard, P. and Grellier, S., Invariant Tori for the cubic Szegő equation, Invent. Math. 187 (2012), 707–754.Google Scholar
Hartman, P., On completely continuous Hankel matrices, Proc. Amer. Math. Soc. 9 (1958), 862–866.Google Scholar
Kronecker, L., Zur Theorie der Elimination einer Variabeln aus zwei algebraischen Gleichungen, Monatsber. Königl. Preuss. Akad. Wiss. (Berlin) (1881), 535–600, Reprinted in Leopold Kronecker’s Werke, vol. 2, 113–192, Chelsea, 1968.Google Scholar
Lax, P., Integrals of nonlinear equations of evolution and solitary waves, Comm. Pure Appl. Math. 21 (1968), 467–490.Google Scholar
Lax, P., Periodic solutions of the KdV equation, Comm. Pure Appl. Math. 28 (1975), 141–188.Google Scholar
Megretskii, A. V., Peller, V. V. and Treil, S. R., The inverse problem for selfadjoint Hankel operators, Acta Math. 174 (1995), 241–309.Google Scholar
Nehari, Z., On bounded bilinear forms, Ann. of Math. (2) 65 (1957), 153–162.Google Scholar
Nikolskii, N. K., Operators, functions, and systems: an easy reading. Vol. 1. Hardy, Hankel, and Toeplitz, Mathematical Surveys and Monographs, Volume Volume 92 (American Mathematical Society, Providence, RI, 2002), Translated from the French by Andreas Hartmann.Google Scholar
Nikolskii, N. K., Treatise on the shift operator, in Spectral function theory. With an appendix by S. V. Khrushchëv and V. V. Peller, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], Volume Volume 273 (Springer-Verlag, Berlin, 1986), Translated from the Russian by Jaak Peetre.Google Scholar
Peller, V. V., Hankel operators of class ${\mathfrak{S}}_{p} $ and their applications (rational approximation, Gaussian processes, the problem of majorization of operators), Math. USSR Sb. 41 (1982), 443–479.CrossRefGoogle Scholar
Peller, V. V., Hankel operators and their applications, Springer Monographs in Mathematics (Springer-Verlag, New York, 2003).Google Scholar
Rudin, W., Real and complex analysis, 2nd edn (Mac Graw Hill, 1980).Google Scholar
Treil, S. R., Moduli of Hankel operators and a problem of Peller–Khrushchëv, Dokl. Akad. Nauk SSSR 283 (5) (1985), 1095–1099 (in Russian); English transl. in Soviet Math. Dokl. 32 (1985), 293–297.Google Scholar
Treil, S. R., Moduli of Hankel operators and the V. V. Peller–S. Kh. Khrushchëv problem, Investigations on linear operators and the theory of functions, XIV, Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. (LOMI) 141 (1985), 39–55(in Russian).Google Scholar
Zakharov, V. E. and Shabat, A. B., Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media, Soviet Phys. JETP 34 (1) (1972), 62–69.Google Scholar