Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-24T19:05:30.976Z Has data issue: false hasContentIssue false
  • English
  • Français

ON CLEAN LAURENT SERIES RINGS

Part of: Homological methods Local rings and generalizations Rings and algebras arising under various constructions Conditions on elements

Published online by Cambridge University Press:  18 July 2013

YIQIANG ZHOU  and
MICHAŁ ZIEMBOWSKI
YIQIANG ZHOU
Affiliation:
Department of Mathematics and Statistics, Memorial University of Newfoundland, St.John’s, Canada Nfld A1C 5S7 email zhou@mun.ca
MICHAŁ ZIEMBOWSKI*
Affiliation:
Faculty of Mathematics and Information Science, Warsaw University of Technology, 00-662 Warsaw, Poland
*
✉m.ziembowski@mini.pw.edu.pl
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Here we prove that, for a 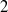$2$-primal ring 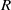$R$, the Laurent series ring 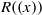$R((x))$ is a clean ring if and only if 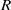$R$ is a semiregular ring with 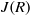$J(R)$ nil. This disproves the claim in K. I. Sonin [‘Semiprime and semiperfect rings of Laurent series’, Math. Notes 60 (1996), 222–226] that the Laurent series ring over a clean ring is again clean. As an application of the result, it is shown that, for a 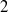$2$-primal ring 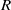$R$, 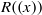$R((x))$ is semiperfect if and only if 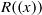$R((x))$ is semiregular if and only if 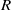$R$ is semiperfect with 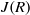$J(R)$ nil.

Keywords

clean ringLaurent series ringsemiregular ringsemiperfect ring2-primal ringnil Jacobson radical

MSC classification

Secondary: 16S99: None of the above, but in this section 16U99: None of the above, but in this section 16E50: von Neumann regular rings and generalizations 16L30: Noncommutative local and semilocal rings, perfect rings
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 95 , Issue 3 , December 2013 , pp. 421 - 427
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Goodearl, K. R. and Warfield, R. B. Jr, ‘Algebras over zero-dimensional rings’, Math. Ann. 223 (1976), 168–187.CrossRefGoogle Scholar
Han, J. and Nicholson, W. K., ‘Extensions of clean rings’, Comm. Algebra 29 (6) (2001), 2589–2595.CrossRefGoogle Scholar
Lam, T. Y., Exercises in Classical Ring Theory, Problem Books in Mathematics (Springer, Berlin–Heidelberg–New York, 1995).CrossRefGoogle Scholar
Nicholson, W. K., ‘Lifting idempotents and exchange rings’, Trans. Amer. Math. Soc. 229 (1977), 269–278.CrossRefGoogle Scholar
Nicholson, W. K. and Zhou, Y., ‘Rings in which elements are uniquely the sum of an idempotent and a unit’, Glasg. Math. J. 46 (2004), 227–236.CrossRefGoogle Scholar
Sonin, K. I., ‘Regular rings of skew Laurent series’, Fundam. Prikl. Mat. 1 (2) (1995), 565–568.Google Scholar
Sonin, K. I., ‘Semiprime and semiperfect rings of Laurent series’, Math. Notes 60 (1996), 222–226.CrossRefGoogle Scholar
Tuganbaev, A. A., ‘The Jacobson radical of the Laurent series ring’, J. Math. Sci. 149 (2) (2008), 1182–1186.CrossRefGoogle Scholar
Warfield, R. B. Jr, ‘Exchange rings and decompositions of modules’, Math. Ann. 199 (1972), 31–36.CrossRefGoogle Scholar
Ziembowski, M., ‘Laurent series ring over semiperfect ring can not be semiperfect’, Comm. Algebra, to appear, doi:10.1080/00927872.2012.720324.CrossRefGoogle Scholar