Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bell, J. L.
1974.
On Compact Cardinals.
Mathematical Logic Quarterly,
Vol. 20,
Issue. 25-27,
p.
389.
1974.
Set Theory - An Introduction to Large Cardinals.
Vol. 76,
Issue. ,
p.
319.
Boos, William
1975.
⊨ISILC Logic Conference.
Vol. 499,
Issue. ,
p.
25.
Galvin, Fred
and
Prikry, Karel
1976.
Infinitary jonsson algebras and partition relations.
Algebra Universalis,
Vol. 6,
Issue. 1,
p.
367.
Kunen, Kenneth
1977.
HANDBOOK OF MATHEMATICAL LOGIC.
Vol. 90,
Issue. ,
p.
371.
Wang, Hao
1977.
Logic, Foundations of Mathematics, and Computability Theory.
p.
309.
Rucker, Rudolf v.B.
1977.
Logic Colloquium 76, Proceedings of a conference.
Vol. 87,
Issue. ,
p.
567.
Kanamori, A.
and
Magidor, M.
1978.
Higher Set Theory.
Vol. 669,
Issue. ,
p.
99.
Kanamori, A.
1978.
Logic Colloquium '77.
Vol. 96,
Issue. ,
p.
145.
Solovay, Robert M.
Reinhardt, William N.
and
Kanamori, Akihiro
1978.
Strong axioms of infinity and elementary embeddings.
Annals of Mathematical Logic,
Vol. 13,
Issue. 1,
p.
73.
1978.
Vol. 79,
Issue. ,
p.
596.
Tall, Franklin D.
1980.
Surveys in General Topology.
p.
445.
Laver, Richard
1982.
Logic Colloquium '80 - Papers intended for the European Summer Meeting of the Association for Symbolic Logic.
Vol. 108,
Issue. ,
p.
173.
Drake, F. R.
1985.
How recent work in mathematical logic relates to the foundations of mathematics.
The Mathematical Intelligencer,
Vol. 7,
Issue. 4,
p.
27.
Laver, Richard
1992.
The left distributive law and the freeness of an algebra of elementary embeddings.
Advances in Mathematics,
Vol. 91,
Issue. 2,
p.
209.
Shioya, Masahiro
1994.
Infinitary J�nsson functions and elementary embeddings.
Archive for Mathematical Logic,
Vol. 33,
Issue. 2,
p.
81.
Zapletal, Jindrich
1996.
A new proof of Kunen’s inconsistency.
Proceedings of the American Mathematical Society,
Vol. 124,
Issue. 7,
p.
2203.
Jech, Thomas
1997.
Large Ordinals.
Advances in Mathematics,
Vol. 125,
Issue. 2,
p.
155.
Laver, Richard
1997.
Implications between strong large cardinal axioms.
Annals of Pure and Applied Logic,
Vol. 90,
Issue. 1-3,
p.
79.
Corazza, Paul
2000.
The wholeness axiom and Laver sequences.
Annals of Pure and Applied Logic,
Vol. 105,
Issue. 1-3,
p.
157.
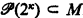 , then κ would be the κth measurable cardinal; in general, the wider we assume M to be, the larger κ must be.
, then κ would be the κth measurable cardinal; in general, the wider we assume M to be, the larger κ must be.



