Article contents
Omitting types, type spectrums, and decidability1
Published online by Cambridge University Press: 12 March 2014
Extract
Notations, conventions, and definitions. {μi∣i < ω} will be an effective enumeration of all partial recursive μi{ω → 2. A type of a theory T will be a set of formulas in the language of T, in finitely many free variables, which is consistent with T. A complete type is a maximal type in some fixed number of free variables. A type is recursive if, relative to some effective enumeration of the formulas of the language, the characteristic function for the type is recursive. A set ψ of recursive types has property P if some set of indices of characteristic functions for all the types in ψ has property P. So, for example, we might say that a set of recursive types is 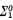 . If
. If 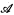 is an L-structure, then the type spectrum of
is an L-structure, then the type spectrum of 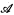 , denoted ‘TySp(
, denoted ‘TySp(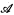 )’, is the set of complete types realized in
)’, is the set of complete types realized in 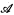 (we will assume that an n-type has formulas with free variables among {x1, …, xn}). A type spectrum for a theory T is a type spectrum of some model of T. ‘TySp0(T)’ will denote the set of principal types of T.
(we will assume that an n-type has formulas with free variables among {x1, …, xn}). A type spectrum for a theory T is a type spectrum of some model of T. ‘TySp0(T)’ will denote the set of principal types of T.
We will assume that the reader is familiar with Henkin constructions of models, and of passing from a maximal consistent set of sentences, with “Henkin constants”, to a model. In particular, for a theory T in L we will let {ai∣i < ω} be new distinct constant symbols, and {φi < ω} a list of all sentences in the expanded language. ‘ΔN’ will denote the elementary diagram constructed at stage N, and 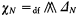 .
.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1983
Footnotes
The preparation of this paper was partially supported by Grant NSF-MCS77-0O802.
References
BIBLIOGRAPHY
- 14
- Cited by




