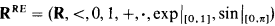Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bianconi, Ricardo
1991.
Model completeness results for elliptic and abelian functions.
Annals of Pure and Applied Logic,
Vol. 54,
Issue. 2,
p.
121.
Richardson, Daniel
1991.
Wu's method and the Khovanskii finiteness theorem.
Journal of Symbolic Computation,
Vol. 12,
Issue. 2,
p.
127.
Richardson, Daniel
1992.
Computer Graphics and Mathematics.
p.
121.
Richardson, Daniel
1992.
Computing the topology of a bounded non algebraic curve in the plane.
Journal of Symbolic Computation,
Vol. 14,
Issue. 6,
p.
619.
van den Dries, Lou
and
Miller, Chris
1994.
On the real exponential field with restricted analytic functions.
Israel Journal of Mathematics,
Vol. 85,
Issue. 1-3,
p.
19.
Miller, Chris
1994.
Expansions of the real field with power functions.
Annals of Pure and Applied Logic,
Vol. 68,
Issue. 1,
p.
79.
Wilkie, A.
1996.
Model completeness results for expansions of the ordered field of real numbers by restricted Pfaffian functions and the exponential function.
Journal of the American Mathematical Society,
Vol. 9,
Issue. 4,
p.
1051.
PETERZIL, YA'ACOV
and
STARCHENKO, SERGEI
2003.
EXPANSIONS OF ALGEBRAICALLY CLOSED FIELDS II: FUNCTIONS OF SEVERAL VARIABLES.
Journal of Mathematical Logic,
Vol. 03,
Issue. 01,
p.
1.
Miller, Daniel
2006.
A preparation theorem for Weierstrass systems.
Transactions of the American Mathematical Society,
Vol. 358,
Issue. 10,
p.
4395.
Sfouli, Hassan
2010.
Definability and nondefinability results for certain o-minimal structures.
Mathematical Logic Quarterly,
Vol. 56,
Issue. 5,
p.
503.
Miller, Chris
2012.
Lecture Notes on O-Minimal Structures and Real Analytic Geometry.
Vol. 62,
Issue. ,
p.
43.
Sfouli, Hassan
2012.
On the Elementary Theory of Restricted Real and Imaginary Parts of Holomorphic Functions.
Notre Dame Journal of Formal Logic,
Vol. 53,
Issue. 1,
Tychonievich, Michael A.
2012.
The Set of Restricted Complex Exponents for Expansions of the Reals.
Notre Dame Journal of Formal Logic,
Vol. 53,
Issue. 2,
Kaiser, Tobias
2013.
Integration of semialgebraic functions and integrated Nash functions.
Mathematische Zeitschrift,
Vol. 275,
Issue. 1-2,
p.
349.
Parusiński, Adam
and
Rolin, Jean-Philippe
2014.
A Note on the Weierstrass Preparation Theorem in Quasianalytic Local Rings.
Canadian Mathematical Bulletin,
Vol. 57,
Issue. 3,
p.
614.
Wilkie, A. J.
2014.
Model Theory in Algebra, Analysis and Arithmetic.
Vol. 2111,
Issue. ,
p.
35.
Kaiser, Tobias
2014.
Multivariate Puiseux Rings Induced by a Weierstrass System and Twisted Group Rings.
Communications in Algebra,
Vol. 42,
Issue. 11,
p.
4619.
Macintyre, Angus
2016.
Turing meets Schanuel.
Annals of Pure and Applied Logic,
Vol. 167,
Issue. 10,
p.
901.
Kaiser, Tobias
2016.
Global complexification of real analytic globally subanalytic functions.
Israel Journal of Mathematics,
Vol. 213,
Issue. 1,
p.
139.
Miller, Chris
2017.
Logic Colloquium '01.
p.
281.