Article contents
Higher order reflection principles
Published online by Cambridge University Press: 12 March 2014
Extract
In [1] and [2] there is a development of a class theory, whose axioms were formulated by Bernays and based on a reflection principle. See [3]. These axioms are formulated in first order logic with ∈:
(A1) Extensionality.
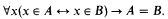
(A2) Class specification. If ϕ is a formula and A is not free in ϕ, then
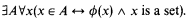
Note that “x is a set“ can be written as “∃u(x ∈ u)”.
(A3) Subsets.
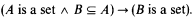
Note also that “B ⊆ A” can be written as “∀x(x ∈ B → x ∈ A)”.
(A4) Reflection principle. If ϕ(x) is a formula, then

where “u is a transitive set” is the formula “∃v(u ∈ v) ∧ ∀x∀y(x ∈ y ∧ y ∈ u → x ∈ u)” and ϕPu is the formula ϕ relativized to subsets of u.
(A5) Foundation.
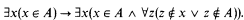
(A6) Choice for sets.
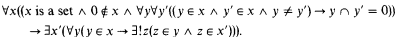
We denote by B1 the theory with axioms (A1) to (A6).
The existence of weakly compact and 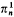 -indescribable cardinals for every n is established in B1 by the method of defining all metamathematical concepts for B1 in a weaker theory of classes where the natural numbers can be defined and using the reflection principle to reflect the satisfaction relation; see [1]. There is a proof of the consistency of B1 assuming the existence of a measurable cardinal; see [4] and [5]. In [6] several set and class theories with reflection principles are developed. In them, the existence of inaccessible cardinals and some kinds of indescribable cardinals can be proved; and also there is a generalization of indescribability for higher-order languages using only class parameters.
-indescribable cardinals for every n is established in B1 by the method of defining all metamathematical concepts for B1 in a weaker theory of classes where the natural numbers can be defined and using the reflection principle to reflect the satisfaction relation; see [1]. There is a proof of the consistency of B1 assuming the existence of a measurable cardinal; see [4] and [5]. In [6] several set and class theories with reflection principles are developed. In them, the existence of inaccessible cardinals and some kinds of indescribable cardinals can be proved; and also there is a generalization of indescribability for higher-order languages using only class parameters.
The purpose of this work is to develop higher order reflection principles, including higher order parameters, in order to obtain other large cardinals.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1989
References
REFERENCES
- 3
- Cited by




