Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Shore, Richard A.
1988.
Defining jump classes in the degrees below 0’.
Proceedings of the American Mathematical Society,
Vol. 104,
Issue. 1,
p.
287.
Cooper, S. Barry
Lempp, Steffen
and
Watson, Philip
1989.
Weak density and cupping in the d-r.e. degrees.
Israel Journal of Mathematics,
Vol. 67,
Issue. 2,
p.
137.
Cooper, S. Barry
1990.
The jump is definable in the structure of the degrees of unsolvability.
Bulletin of the American Mathematical Society,
Vol. 23,
Issue. 1,
p.
151.
Kumabe, Masahiro
1993.
Generic degrees are complemented.
Annals of Pure and Applied Logic,
Vol. 59,
Issue. 3,
p.
257.
Schaeffer, Benjamin
1998.
Dynamic notions of genericity and array noncomputability.
Annals of Pure and Applied Logic,
Vol. 95,
Issue. 1-3,
p.
37.
Cooper, S. Barry
1999.
Handbook of Computability Theory.
Vol. 140,
Issue. ,
p.
121.
Chong, C. T.
Qian, Lei
Slaman, Theodore A.
and
Yang, Yue
2001.
∑2 Induction and infinite injury priority arguments, part III: Prompt sets, minimal pairs and Shoenfield’s Conjecture.
Israel Journal of Mathematics,
Vol. 121,
Issue. 1,
p.
1.
Cooper, S. B.
and
Li, Angsheng
2002.
Splitting and cone avoidance in the D.C.E. degrees.
Science China Mathematics,
Vol. 45,
Issue. 9,
p.
1135.
Wu, Guohua
2004.
Quasi‐complements of the cappable degrees.
Mathematical Logic Quarterly,
Vol. 50,
Issue. 2,
p.
189.
Lewis, Andrew E. M.
2005.
The minimal complementation property above 0′.
Mathematical Logic Quarterly,
Vol. 51,
Issue. 5,
p.
470.
Li, Angsheng
Song, Yan
and
Wu, Guohua
2006.
Theory and Applications of Models of Computation.
Vol. 3959,
Issue. ,
p.
721.
Lewis, Andrew
2007.
A single minimal complement for the c.e. degrees.
Transactions of the American Mathematical Society,
Vol. 359,
Issue. 12,
p.
5817.
Soskova, Mariya Ivanova
and
Cooper, S. Barry
2007.
Theory and Applications of Models of Computation.
Vol. 4484,
Issue. ,
p.
199.
Wu, Guohua
2007.
Intervals containing exactly one c.e. degree.
Annals of Pure and Applied Logic,
Vol. 146,
Issue. 1,
p.
91.
Yamaleev, M. M.
2010.
Strong noncuppability in low computably enumerable degrees.
Russian Mathematics,
Vol. 54,
Issue. 4,
p.
72.
Liu, Jiang
and
Wu, Guohua
2010.
Programs, Proofs, Processes.
Vol. 6158,
Issue. ,
p.
266.
Lewis, Andrew
2011.
A note on the join property.
Proceedings of the American Mathematical Society,
Vol. 140,
Issue. 2,
p.
707.
Lewis, A. E. M.
2012.
Properties of the jump classes.
Journal of Logic and Computation,
Vol. 22,
Issue. 4,
p.
845.
Day, Adam
and
Miller, Joseph
2014.
Cupping with random sets.
Proceedings of the American Mathematical Society,
Vol. 142,
Issue. 8,
p.
2871.
Slaman, Theodore A.
2017.
Logic Colloquium 2000.
p.
365.
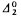 degree has a complement below 0′. We show that a 1-generic complement for each
degree has a complement below 0′. We show that a 1-generic complement for each 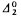 set of degree between 0 and 0′ can be found uniformly. Moreover, the methods just as easily can be used to produce a complement whose jump has the degree of any real recursively enumerable in and above ∅′. In the second half of the paper, we show that the complementation of the degrees below 0′ does not extend to all recursively enumerable degrees. Namely, there is a pair of recursively enumerable degrees a above b such that no degree strictly below a joins b above a. (This result is independently due to S. B. Cooper.) We end with some open problems.
set of degree between 0 and 0′ can be found uniformly. Moreover, the methods just as easily can be used to produce a complement whose jump has the degree of any real recursively enumerable in and above ∅′. In the second half of the paper, we show that the complementation of the degrees below 0′ does not extend to all recursively enumerable degrees. Namely, there is a pair of recursively enumerable degrees a above b such that no degree strictly below a joins b above a. (This result is independently due to S. B. Cooper.) We end with some open problems.



