Hostname: page-component-8448b6f56d-42gr6 Total loading time: 0 Render date: 2024-04-19T11:31:23.682Z Has data issue: false hasContentIssue false
  • English
  • Français

Phase semantics and sequent calculus for pure noncommutative classical linear propositional logic

Published online by Cambridge University Press:  12 March 2014

V. Michele Abrusci
V. Michele Abrusci*
Affiliation:
Filosofia Della Scienza—Logica Matematica, Dipartimento di Scienze Filosofiche, Università di Bari, 70121 Bari, Italy
Get access Rights & Permissions [Opens in a new window]

Extract

The linear logic introduced in [3] by J.-Y. Girard keeps one of the so-called structural rules of the sequent calculus: the exchange rule. In a one-sided sequent calculus this rule can be formulated as

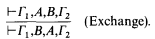
The exchange rule allows one to disregard the order of the assumptions and the order of the conclusions of a proof, and this means, when the proof corresponds to a logically correct program, to disregard the order in which the inputs and the outputs occur in a program.

In the linear logic introduced in [3], the exchange rule allows one to prove the commutativity of the multiplicative connectives, conjunction (⊗) and disjunction (⅋). Due to the presence of the exchange rule in linear logic, in the phase semantics for linear logic one starts with a commutative monoid. So, the usual linear logic may be called commutative linear logic.

The aim of the investigations underlying this paper was to see, first, what happens when we remove the exchange rule from the sequent calculus for the linear propositional logic at all, and then, how to recover the strength of the exchange rule by means of exponential connectives (in the same way as by means of the exponential connectives ! and ? we recover the strength of the weakening and contraction rules).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 56 , Issue 4 , December 1991 , pp. 1403 - 1451
Copyright
Copyright © Association for Symbolic Logic 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Abrusci, V. M., Noncommutative intuitionistic linear propositional logic, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 36 (1990), pp. 297–318.CrossRefGoogle Scholar
[2]Abrusci, V. M., Cut-elimination theorem for pure noncommutative classical linear propositional logic, preprint, Università di Bari, Bari, 1990.Google Scholar
[3]Girard, J.-Y., Linear logic, Theoretical Computer Science, vol. 50 (1987), pp. 1–102.CrossRefGoogle Scholar
[4]Girard, J.-Y., Towards a geometry of interaction, Categories in computer science and logic, Contemporary Mathematics, vol. 92, American Mathematical Society, Providence, Rhode Island, 1989, pp. 69–108.CrossRefGoogle Scholar
[5]Niefeld, S. B. and Rosenthal, K. I., Constructing locales from quantales, Mathematical Proceedings of the Cambridge Philosophical Society, vol. 104 (1988), pp. 215–234.CrossRefGoogle Scholar
[6]Yetter, D. N., Quantales and (noncommutative) linear logic, this Journal, vol. 55 (1990), pp. 41–64.Google Scholar