Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Lion, Jean-Marie
and
Speissegger, Patrick
2000.
Analytic stratification in the Pfaffian closure of an o-minimal structure.
Duke Mathematical Journal,
Vol. 103,
Issue. 2,
Tressl, Marcus
2005.
The elementary theory of Dedekind cuts in polynomially bounded structures.
Annals of Pure and Applied Logic,
Vol. 135,
Issue. 1-3,
p.
113.
Mellor, T.
2006.
Imaginaries in real closed valued fields.
Annals of Pure and Applied Logic,
Vol. 139,
Issue. 1-3,
p.
230.
Miller, Chris
and
Tyne, James
2006.
Expansions of o-Minimal Structures by Iteration Sequences.
Notre Dame Journal of Formal Logic,
Vol. 47,
Issue. 1,
Dolich, Alfred
2007.
A Note on Weakly O-Minimal Structures and Definable Completeness.
Notre Dame Journal of Formal Logic,
Vol. 48,
Issue. 2,
Maříková, Jana
2009.
The structure on the real field generated by the standard part map on an o-minimal expansion of a real closed field.
Israel Journal of Mathematics,
Vol. 171,
Issue. 1,
p.
175.
Dolich, Alfred
Miller, Chris
and
Steinhorn, Charles
2009.
Structures having o-minimal open core.
Transactions of the American Mathematical Society,
Vol. 362,
Issue. 3,
p.
1371.
Miller, Chris
2012.
Lecture Notes on O-Minimal Structures and Real Analytic Geometry.
Vol. 62,
Issue. ,
p.
43.
Mislove, Michael
2012.
2010–2011 Winter Meeting of the Association for Symbolic Logic.
The Bulletin of Symbolic Logic,
Vol. 18,
Issue. 1,
p.
142.
Eivazloo, Jafar S.
and
Tari, Somayyeh
2014.
Tame properties of sets and functions definable in weakly o-minimal structures.
Archive for Mathematical Logic,
Vol. 53,
Issue. 3-4,
p.
433.
Laskowski, Michael C.
and
Shaw, Christopher S.
2016.
Definable choice for a class of weakly o-minimal theories.
Archive for Mathematical Logic,
Vol. 55,
Issue. 5-6,
p.
735.
Caulfield, Erin
2017.
On expansions of the real field by complex subgroups.
Annals of Pure and Applied Logic,
Vol. 168,
Issue. 6,
p.
1308.
García Ramírez, Erick
2017.
Non‐archimedean stratifications of tangent cones.
Mathematical Logic Quarterly,
Vol. 63,
Issue. 3-4,
p.
299.
Miller, Chris
2017.
Logic Colloquium '01.
p.
281.
Yin, Yimu
2017.
Generalized Euler characteristic in power-bounded T-convex valued fields.
Compositio Mathematica,
Vol. 153,
Issue. 12,
p.
2591.
Ealy, Clifton
Haskell, Deirdre
and
Maříková, Jana
2019.
Residue Field Domination in Real Closed Valued Fields.
Notre Dame Journal of Formal Logic,
Vol. 60,
Issue. 3,
García Ramírez, Erick
2020.
Definable Functions and Stratifications in Power-Bounded T -Convex Fields.
Notre Dame Journal of Formal Logic,
Vol. 61,
Issue. 3,
Halevi, Yatir
Hasson, Assaf
and
Peterzil, Ya'acov
2022.
Interpretable fields in various valued fields.
Advances in Mathematics,
Vol. 404,
Issue. ,
p.
108408.
Kaplan, Elliot
2022.
T-convex T-differential fields and their immediate extensions.
Pacific Journal of Mathematics,
Vol. 320,
Issue. 2,
p.
261.
Cluckers, Raf
Halupczok, Immanuel
and
Rideau-Kikuchi, Silvain
2022.
Hensel minimality I.
Forum of Mathematics, Pi,
Vol. 10,
Issue. ,
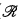 , V) ⊨ Tconvex, let
, V) ⊨ Tconvex, let 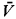 = V/m(V) be the residue field, with residue class map x ↦
= V/m(V) be the residue field, with residue class map x ↦ 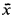 : V ↦
: V ↦ 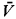 , and let υ:
, and let υ: 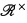 → Γ be the associated valuation. “Definable” will mean “definable with parameters”. The main goal of this article is to determine the structure induced by (
→ Γ be the associated valuation. “Definable” will mean “definable with parameters”. The main goal of this article is to determine the structure induced by (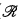 , V) on its residue field
, V) on its residue field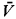 and on its value group Γ. In [9] we expanded the ordered field
and on its value group Γ. In [9] we expanded the ordered field 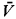 to a model of T as follows. Take a tame elementary substructure
to a model of T as follows. Take a tame elementary substructure 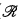 ′ of
′ of 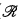 such that R′ ⊆ V and R′ maps bijectively onto
such that R′ ⊆ V and R′ maps bijectively onto 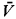 under the residue class map, and make this bijection into an isomorphism
under the residue class map, and make this bijection into an isomorphism 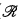 ′ ≌
′ ≌ 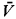 of T-models. (We showed such
of T-models. (We showed such  ′ exists, and that this gives an expansion of
′ exists, and that this gives an expansion of 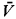 to a T-model that is independent of the choice of
to a T-model that is independent of the choice of 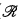 ′.).
′.).



