Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lafitte, Grégory
2001.
Fundamentals of Computation Theory.
Vol. 2138,
Issue. ,
p.
252.
Visser, Albert
2002.
Handbook of Philosophical Logic.
p.
149.
Wiedermann, Jiří
and
van Leeuwen, Jan
2002.
Unconventional Models of Computation.
Vol. 2509,
Issue. ,
p.
287.
Copeland, B. Jack
2002.
Unconventional Models of Computation.
Vol. 2509,
Issue. ,
p.
15.
Lafitte, Grégory
2002.
Foundations of Information Technology in the Era of Network and Mobile Computing.
p.
267.
Cotogno, Paolo
2003.
Hypercomputation and the Physical Church‐Turing Thesis.
The British Journal for the Philosophy of Science,
Vol. 54,
Issue. 2,
p.
181.
Burgin, M.
2003.
Nonlinear phenomena in spaces of algorithms.
International Journal of Computer Mathematics,
Vol. 80,
Issue. 12,
p.
1449.
Hamkins, Joel David
and
Welch, Philip D.
2003.
Pf ≠ NPf for almost all f.
Mathematical Logic Quarterly,
Vol. 49,
Issue. 5,
p.
536.
Namikawa, Jun
and
Hashimoto, Takashi
2004.
Dynamics and computation in functional shifts.
Nonlinearity,
Vol. 17,
Issue. 4,
p.
1317.
2004.
2003 European Summer Meeting of the Association for Symbolic Logic. Logic Colloquim '03.
Bulletin of Symbolic Logic,
Vol. 10,
Issue. 02,
p.
234.
Lenzi, Giacomo
and
Monteleone, Erich
2004.
On Fixpoint Arithmetic and Infinite Time Turing Machines.
Information Processing Letters,
Vol. 91,
Issue. 3,
p.
121.
Bringsjord, Selmer
and
Arkoudas, Konstantine
2004.
The modal argument for hypercomputing minds.
Theoretical Computer Science,
Vol. 317,
Issue. 1-3,
p.
167.
Burgin, Mark
and
Klinger, Allen
2004.
Three aspects of super-recursive algorithms and hypercomputation or finding black swans.
Theoretical Computer Science,
Vol. 317,
Issue. 1-3,
p.
1.
Wells, Benjamin
2004.
Hypercomputation by definition.
Theoretical Computer Science,
Vol. 317,
Issue. 1-3,
p.
191.
Welch, P. D.
2004.
On the Possibility, or Otherwise, of Hypercomputation.
The British Journal for the Philosophy of Science,
Vol. 55,
Issue. 4,
p.
739.
Shagrir, Oron
2004.
Super-tasks, accelerating Turing machines and uncomputability.
Theoretical Computer Science,
Vol. 317,
Issue. 1-3,
p.
105.
Ziegler, Martin
2005.
Computational Power of Infinite Quantum Parallelism.
International Journal of Theoretical Physics,
Vol. 44,
Issue. 11,
p.
2059.
Durand-Lose, Jérôme
2005.
New Computational Paradigms.
Vol. 3526,
Issue. ,
p.
106.
Hamkins, Joel David
2005.
New Computational Paradigms.
Vol. 3526,
Issue. ,
p.
180.
Koepke, Peter
2005.
New Computational Paradigms.
Vol. 3526,
Issue. ,
p.
223.




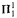 set. for example, is decidable by such machines, and the semi-decidable sets form a portion of the
set. for example, is decidable by such machines, and the semi-decidable sets form a portion of the 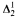 sets. Our oracle concept leads to a notion of relative computability for sets of reals and a rich degree structure, stratified by two natural jump operators.
sets. Our oracle concept leads to a notion of relative computability for sets of reals and a rich degree structure, stratified by two natural jump operators.