Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
2007.
Residuated Lattices: An Algebraic Glimpse at Substructural Logics.
Vol. 151,
Issue. ,
p.
479.
2007.
Residuated Lattices: An Algebraic Glimpse at Substructural Logics.
Vol. 151,
Issue. ,
p.
463.
van Alten, C. J.
2009.
Completion and finite embeddability property for residuated ordered algebras..
Algebra universalis,
Vol. 62,
Issue. 4,
p.
419.
Raftery, J. G.
2011.
A perspective on the algebra of logic.
Quaestiones Mathematicae,
Vol. 34,
Issue. 3,
p.
275.
Raftery, J. G.
2011.
Contextual Deduction Theorems.
Studia Logica,
Vol. 99,
Issue. 1-3,
p.
279.
Horčík, Rostislav
2015.
Word problem for knotted residuated lattices.
Journal of Pure and Applied Algebra,
Vol. 219,
Issue. 5,
p.
1548.
Cardona, R.
and
Galatos, N.
2015.
The finite embeddability property for noncommutative knotted extensions of RL.
International Journal of Algebra and Computation,
Vol. 25,
Issue. 03,
p.
349.
Cardona, Riquelmi
and
Galatos, Nikolaos
2017.
The FEP for some varieties of fully distributive knotted residuated lattices.
Algebra universalis,
Vol. 78,
Issue. 3,
p.
363.
Gil-Férez, José
Jipsen, Peter
and
Metcalfe, George
2020.
Structure theorems for idempotent residuated lattices.
Algebra universalis,
Vol. 81,
Issue. 2,
Gil-Férez, José
Spada, Luca
Tsinakis, Constantine
and
Zhou, Hongjun
2020.
Join-completions of partially ordered algebras.
Annals of Pure and Applied Logic,
Vol. 171,
Issue. 10,
p.
102842.
Raftery, James G.
2022.
Hiroakira Ono on Substructural Logics.
Vol. 23,
Issue. ,
p.
27.
Horčík, Rostislav
2022.
Hiroakira Ono on Substructural Logics.
Vol. 23,
Issue. ,
p.
273.
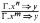 . It is proved that the class of algebraic models for such a logic has the finite embeddability property, meaning that every finite partial subalgebra of an algebra in the class can be embedded into a finite full algebra in the class. It follows that each such logic has the finite model property with respect to its algebraic semantics and hence that the logic is decidable.
. It is proved that the class of algebraic models for such a logic has the finite embeddability property, meaning that every finite partial subalgebra of an algebra in the class can be embedded into a finite full algebra in the class. It follows that each such logic has the finite model property with respect to its algebraic semantics and hence that the logic is decidable.



