Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Montalbán, Antonio
2006.
Equivalence between Fraïssé’s conjecture and Jullien’s theorem.
Annals of Pure and Applied Logic,
Vol. 139,
Issue. 1-3,
p.
1.
MONTALBÁN, ANTONIO
2006.
INDECOMPOSABLE LINEAR ORDERINGS AND HYPERARITHMETIC ANALYSIS.
Journal of Mathematical Logic,
Vol. 06,
Issue. 01,
p.
89.
COLE, JOSHUA A.
and
SIMPSON, STEPHEN G.
2007.
MASS PROBLEMS AND HYPERARITHMETICITY.
Journal of Mathematical Logic,
Vol. 07,
Issue. 02,
p.
125.
Montalbán, Antonio
2007.
On the Equimorphism Types of Linear Orderings.
Bulletin of Symbolic Logic,
Vol. 13,
Issue. 1,
p.
71.
Montalbán, Antonio
2011.
Open Questions in Reverse Mathematics.
The Bulletin of Symbolic Logic,
Vol. 17,
Issue. 3,
p.
431.
Montalbán, Antonio
2013.
A computability theoretic equivalent to Vaught’s conjecture.
Advances in Mathematics,
Vol. 235,
Issue. ,
p.
56.
MONTALBÁN, ANTONIO
2015.
ANALYTIC EQUIVALENCE RELATIONS SATISFYING HYPERARITHMETIC-IS-RECURSIVE.
Forum of Mathematics, Sigma,
Vol. 3,
Issue. ,
Kanamori, Akihiro
2016.
Laver and set theory.
Archive for Mathematical Logic,
Vol. 55,
Issue. 1-2,
p.
133.
Bazhenov, N. A.
Fokina, E. B.
Rossegger, D.
and
San Mauro, L.
2018.
Computable Bi-Embeddable Categoricity.
Algebra and Logic,
Vol. 57,
Issue. 5,
p.
392.
Fokina, Ekaterina
Rossegger, Dino
and
San Mauro, Luca
2019.
Bi‐embeddability spectra and bases of spectra.
Mathematical Logic Quarterly,
Vol. 65,
Issue. 2,
p.
228.
Bazhenov, Nikolay
Fokina, Ekaterina
Rossegger, Dino
and
San Mauro, Luca
2019.
Degrees of bi-embeddable categoricity of equivalence structures.
Archive for Mathematical Logic,
Vol. 58,
Issue. 5-6,
p.
543.
Bazhenov, Nikolay
Fokina, Ekaterina
Rossegger, Dino
and
San Mauro, Luca
2021.
Degrees of bi-embeddable categoricity.
Computability,
Vol. 10,
Issue. 1,
p.
1.
SHAFER, PAUL
and
TERWIJN, SEBASTIAAN A.
2021.
ORDINAL ANALYSIS OF PARTIAL COMBINATORY ALGEBRAS.
The Journal of Symbolic Logic,
Vol. 86,
Issue. 3,
p.
1154.
Bazhenov, Nikolay
Rossegger, Dino
and
Zubkov, Maxim
2022.
On bi-embeddable categoricity of algebraic structures.
Annals of Pure and Applied Logic,
Vol. 173,
Issue. 3,
p.
103060.
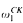 if and only if it is equimorphic to a recursive one. As a corollary of our proof we prove that, given a recursive ordinal α, the partial ordering of equimorphism types of linear orderings of Hausdorff rank at most α ordered by embeddablity is recursively presentable.
if and only if it is equimorphic to a recursive one. As a corollary of our proof we prove that, given a recursive ordinal α, the partial ordering of equimorphism types of linear orderings of Hausdorff rank at most α ordered by embeddablity is recursively presentable.



