Article contents
Combinatorial principles weaker than Ramsey's Theorem for pairs
Published online by Cambridge University Press: 12 March 2014
Abstract
We investigate the complexity of various combinatorial theorems about linear and partial orders, from the points of view of computability theory and reverse mathematics. We focus in particular on the principles ADS (Ascending or Descending Sequence), which states that every infinite linear order has either an infinite descending sequence or an infinite ascending sequence, and CAC (Chain-AntiChain), which states that every infinite partial order has either an infinite chain or an infinite antichain. It is wellknown that Ramsey's Theorem for pairs (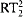 ) splits into a stable version (
) splits into a stable version (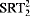 ) and a cohesive principle (COH). We show that the same is true of ADS and CAC, and that in their cases the stable versions are strictly weaker than the full ones (which is not known to be the case for
) and a cohesive principle (COH). We show that the same is true of ADS and CAC, and that in their cases the stable versions are strictly weaker than the full ones (which is not known to be the case for 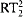 and
and 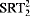 ). We also analyze the relationships between these principles and other systems and principles previously studied by reverse mathematics, such as WKL0, DNR, and BΣ2. We show, for instance, that WKL0 is incomparable with all of the systems we study. We also prove computability-theoretic and conservation results for them. Among these results are a strengthening of the fact, proved by Cholak, Jockusch, and Slaman, that COH is
). We also analyze the relationships between these principles and other systems and principles previously studied by reverse mathematics, such as WKL0, DNR, and BΣ2. We show, for instance, that WKL0 is incomparable with all of the systems we study. We also prove computability-theoretic and conservation results for them. Among these results are a strengthening of the fact, proved by Cholak, Jockusch, and Slaman, that COH is  -conservative over the base system RCA0. We also prove that CAC does not imply DNR which, combined with a recent result of Hirschfeldt, Jockusch. Kjos-Hanssen, Lempp, and Slaman, shows that CAC does not imply
-conservative over the base system RCA0. We also prove that CAC does not imply DNR which, combined with a recent result of Hirschfeldt, Jockusch. Kjos-Hanssen, Lempp, and Slaman, shows that CAC does not imply 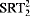 (and so does not imply
(and so does not imply 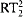 ). This answers a question of Cholak, Jockusch, and Slaman.
). This answers a question of Cholak, Jockusch, and Slaman.
Our proofs suggest that the essential distinction between ADS and CAC on the one hand and 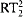 on the other is that the colorings needed for our analysis are in some way transitive. We formalize this intuition as the notions of transitive and semitransitive colorings and show that the existence of homogeneous sets for such colorings is equivalent to ADS and CAC, respectively. We finish with several open questions.
on the other is that the colorings needed for our analysis are in some way transitive. We formalize this intuition as the notions of transitive and semitransitive colorings and show that the existence of homogeneous sets for such colorings is equivalent to ADS and CAC, respectively. We finish with several open questions.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2007
References
REFERENCES
- 68
- Cited by




