Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-18T16:55:42.662Z Has data issue: false hasContentIssue false
  • English
  • Français

Hypergraph sequences as a tool for saturation of ultrapowers

Published online by Cambridge University Press:  12 March 2014

M. E. Malliaris
M. E. Malliaris*
Affiliation:
Department of Mathematics, University of Chicago, 5734 S. University Ave, Chicago, IL 60637, USA, E-mail: mem@math.uchicago.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let T1, T2 be countable first-order theories, Mi ⊨ Ti and 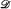any regular ultrafilter on λ ≥ ℵ0. A longstanding open problem of Keisler asks when T2 is more complex than T1, as measured by the fact that for any such λ, 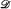, if the ultrapower 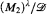realizes all types over sets of size ≤ λ, then so must the ultrapower . In this paper, building on the author's prior work [12] [13] [14], we show that the relative complexity of first-order theories in Keisler's sense is reflected in the relative graph-theoretic complexity of sequences of hypergraphs associated to formulas of the theory. After reviewing prior work on Keisler's order, we present the new construction in the context of ultrapowers, give various applications to the open question of the unstable classification, and investigate the interaction between theories and regularizing sets. We show that there is a minimum unstable theory, a minimum TP2 theory, and that maximality is implied by the density of certain graph edges (between components arising from Szemerédi-regular decompositions) remaining bounded away from 0, 1. We also introduce and discuss flexible ultrafilters, a relevant class of regular ultrafilters which reflect the sensitivity of certain unstable (non low) theories to the sizes of regularizing sets, and prove that any ultrafilter which saturates the minimal TP2 theory is flexible.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 77 , Issue 1 , March 2012 , pp. 195 - 223
Copyright
Copyright © Association for Symbolic Logic 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Baker, J. and Kunen, K., Limits in the uniform ultrafilters, Transactions of the American Mathematical Society, vol. 353 (2001), no. 10, pp. 4083–4093.CrossRefGoogle Scholar
[2]Buechler, S., Lascar strong types in some simple theories, this Journal, vol. 64 (1999), no. 2, pp. 817–824.Google Scholar
[3]Comfort, W. and Negrepontis, S., The theory of ultrafilters, Springer-Verlag, 1974.CrossRefGoogle Scholar
[4]Dow, A., Good and ok ultrafilters, Transactions of the American Mathematical Society, vol. 290 (1985), no. 1, pp. 145–160.CrossRefGoogle Scholar
[5]Džamonja, M. and Shelah, S., On ⊲*-maximality, Annals of Pure and Applied Logic, vol. 125 (2004), pp. 119–158.CrossRefGoogle Scholar
[6]Farah, I., Hart, B., and Sherman, D., Model theory of operator algebras II: model theory, 2010, Arxiv: 1004.0741v1.Google Scholar
[7]Guingona, V., On uniform definability of types over finite sets, 2010, Arxiv: 1005.4924.Google Scholar
[8]Keisler, H. J., Ultraproducts which are not saturated, this Journal, vol. 32 (1967), pp. 23–46.Google Scholar
[9]Kochen, S., Ultraproducts in the theory of models, Annals of Mathematics. Second Series, vol. 74 (1961), no. 2, pp. 221–261.CrossRefGoogle Scholar
[10]Komlós, J. and Simonovitz, M., Szemerédi's regularity lemma and its applications in graph theory, Combinatorics, Paul Erdős is eighty. Volume 2, Bolyai Society Mathematical Studies, Budapest, 1996, pp. 295–352.Google Scholar
[11]Kunen, K., Ultrafilters and independent sets, Transactions of the American Mathematical Society, vol. 172 (1972), pp. 299–306.CrossRefGoogle Scholar
[12]Malliaris, M., Realization of φ-types and Keisler's order, Annals of Pure and Applied Logic, vol. 157 (2009), pp. 220–224.CrossRefGoogle Scholar
[13]Malliaris, M., The characteristic sequence of a first-order formula, this Journal, vol. 75 (2010), no. 4, pp. 1415–1440.Google Scholar
[14]Malliaris, M., Edge distribution and density in the characteristic sequence, Annals of Pure and Applied Logic, vol. 162 (2010), no. 1, pp. 1–19.CrossRefGoogle Scholar
[15]Shelah, S., Simple unstable theories, Annals of Mathematical Logic, vol. 19 (1980), pp. 177–203.CrossRefGoogle Scholar
[16]Shelah, S., Classification theory and the number of non-isomorphic models, revised ed., North-Holland, 1990.Google Scholar
[17]Shelah, S., The universality spectrum: Consistency for more classes, Combinatorics: Paul Erdős is eighty. Volume 1, Bolyai Society Mathematical Studies, Budapest, 1993, pp. 403–420.Google Scholar
[18]Shelah, S., Toward classifying unstable theories, Annals of Pure and Applied Logic, vol. 80 (1996), pp. 229–255.CrossRefGoogle Scholar
[19]Shelah, S. and Usvyatsov, A., More on SOP1and SOP2, Annals of Pure and Applied Logic, vol. 155 (2008), no. 1, pp. 16–31.CrossRefGoogle Scholar