Article contents
Mass Problems and Randomness
Published online by Cambridge University Press: 15 January 2014
Abstract
A mass problem is a set of Turing oracles. If P and Q are mass problems, we say that P is weakly reducible to Q if every member of Q Turing computes a member of P. We say that P is strongly reducible to Q if every member of Q Turing computes a member of P via a fixed Turing functional. The weak degrees and strong degrees are the equivalence classes of mass problems under weak and strong reducibility, respectively. We focus on the countable distributive lattices 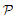 ω and
ω and 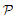 s of weak and strong degrees of mass problems given by nonempty
s of weak and strong degrees of mass problems given by nonempty  subsets of 2ω. Using an abstract Gödel/Rosser incompleteness property, we characterize the
subsets of 2ω. Using an abstract Gödel/Rosser incompleteness property, we characterize the  subsets of 2ω whose associated mass problems are of top degree in
subsets of 2ω whose associated mass problems are of top degree in 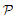 ω and
ω and 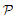 s, respectively Let R be the set of Turing oracles which are random in the sense of Martin-Löf, and let r be the weak degree of R. We show that r is a natural intermediate degree within
s, respectively Let R be the set of Turing oracles which are random in the sense of Martin-Löf, and let r be the weak degree of R. We show that r is a natural intermediate degree within 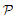 ω. Namely, we characterize r as the unique largest weak degree of a
ω. Namely, we characterize r as the unique largest weak degree of a  subset of 2ω of positive measure. Within
subset of 2ω of positive measure. Within 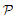 ω we show that r is meet irreducible, does not join to 1, and is incomparable with all weak degrees of nonempty thin perfect
ω we show that r is meet irreducible, does not join to 1, and is incomparable with all weak degrees of nonempty thin perfect  subsets of 2ω. In addition, we present other natural examples of intermediate degrees in
subsets of 2ω. In addition, we present other natural examples of intermediate degrees in 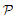 ω. We relate these examples to reverse mathematics, computational complexity, and Gentzen-style proof theory.
ω. We relate these examples to reverse mathematics, computational complexity, and Gentzen-style proof theory.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2005
References
REFERENCES
- 48
- Cited by




