Hostname: page-component-8448b6f56d-42gr6 Total loading time: 0 Render date: 2024-04-24T04:25:20.618Z Has data issue: false hasContentIssue false
  • English
  • Français

Moduli of products of stable varieties

Part of: Families, fibrations Surfaces and higher-dimensional varieties

Published online by Cambridge University Press:  06 September 2013

Bhargav Bhatt ,
Wei Ho ,
Zsolt Patakfalvi  and
Christian Schnell
Bhargav Bhatt*
Affiliation:
School of Mathematics, Institute for Advanced Study, Princeton, NJ 08540, USA
Wei Ho
Affiliation:
Department of Mathematics, Columbia University, NY 10027, USA email who@math.columbia.edu Department of Mathematics, Princeton University, Fine Hall, Washington Road, Princeton, NJ 08544-1000, USA email who@math.columbia.edupzs@princeton.edu
Zsolt Patakfalvi
Affiliation:
Department of Mathematics, Princeton University, Fine Hall, Washington Road, Princeton, NJ 08544-1000, USA email who@math.columbia.edupzs@princeton.edu
Christian Schnell
Affiliation:
Department of Mathematics, Stony Brook University, Stony Brook, NY 11794, USA email christian.schnell@stonybrook.edu
*
bhargav.bhatt@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the moduli space of a product of stable varieties over the field of complex numbers, as defined via the minimal model program. Our main results are: (a) taking products gives a well-defined morphism from the product of moduli spaces of stable varieties to the moduli space of a product of stable varieties; (b) this map is always finite étale; and (c) this map very often is an isomorphism. Our results generalize and complete the work of Van Opstall in dimension 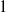$1$. The local results rely on a study of the cotangent complex using some derived algebro-geometric methods, while the global ones use some differential-geometric input.

Keywords

stable varietiesmoduli spacesdeformation theorycotangent complexderived algebraic geometrystable vector bundles

MSC classification

Secondary: 14D05: Structure of families (Picard-Lefschetz, monodromy, etc.) 14D06: Fibrations, degenerations 14D15: Formal methods; deformations 14D20: Algebraic moduli problems, moduli of vector bundles 14D22: Fine and coarse moduli spaces 14D23: Stacks and moduli problems 14J15: Moduli, classification 14J17: Singularities
Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 12 , December 2013 , pp. 2036 - 2070
Copyright
© The Author(s) 2013 

References

Abramovich, D. and Hassett, B., Stable varieties with a twist, in Classification of Algebraic Varieties, EMS Series of Congress Reports (European Mathematical Society, Zurich, 2010), 1–38.Google Scholar
Alexeev, V., Complete moduli in the presence of semiabelian group action, Ann. of Math. (2) 155 (2002), 611–708.CrossRefGoogle Scholar
Alexeev, V. and Pardini, R., Explicit compactifications of moduli spaces of Campedelli and Burniat surfaces, Preprint (2009), arXiv:0901.4431.Google Scholar
Aubin, T., Équations du type Monge–Ampère sur les variétés kähleriennes compactes, C. R. Acad. Sci. Paris Sér. A–B 283 (1976), A119–A121.Google Scholar
Beauville, A., Complex manifolds with split tangent bundle, in Complex Analysis and Algebraic Geometry (de Gruyter, Berlin, 2000), 61–70.Google Scholar
Birkar, C., Cascini, P., Hacon, C. D. and McKernan, J., Existence of minimal models for varieties of log general type, J. Amer. Math. Soc. 23 (2010), 405–468.CrossRefGoogle Scholar
Catanese, F., Connected components of moduli spaces, J. Differential Geom. 24 (1986), 395–399.Google Scholar
Deligne, P. and Illusie, L., Relèvements modulo ${p}^{2} $ et décomposition du complexe de de Rham, Invent. Math. 89 (1987), 247–270.CrossRefGoogle Scholar
Greb, D., Kebekus, S., Kovács, S. J. and Peternell, T., Differential forms on log canonical spaces, Publ. Math. Inst. Hautes Études Sci. 114 (2011), 87–169.Google Scholar
Grothendieck, A., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. II, Publ. Math. Inst. Hautes Études Sci. (1965), 231.Google Scholar
Hacking, P., Compact moduli of plane curves, Duke Math. J. 124 (2004), 213–257.Google Scholar
Hacking, P., Keel, S. and Tevelev, J., Compactification of the moduli space of hyperplane arrangements, J. Algebraic Geom. 15 (2006), 657–680.Google Scholar
Hacking, P., Keel, S. and Tevelev, J., Stable pair, tropical, and log canonical compactifications of moduli spaces of del Pezzo surfaces, Invent. Math. 178 (2009), 173–227.Google Scholar
Hacon, C. and Xu, C., Existence of log canonical closures, Preprint (2011), arXiv:1105.1169.Google Scholar
Hartshorne, R., Generalized divisors on Gorenstein schemes, in Proceedings of Conference on Algebraic Geometry and Ring Theory in honor of Michael Artin, Part III, Antwerp, 1992, K-Theory, vol. 8, (1994), 287–339.Google Scholar
Hassett, B., Stable log surfaces and limits of quartic plane curves, Manuscripta Math. 100 (1999), 469–487.CrossRefGoogle Scholar
Huybrechts, D., An introduction. Complex Geometry, in Universitext (Springer, Berlin, 2005).Google Scholar
Huybrechts, D. and Lehn, M., The geometry of moduli spaces of sheaves, Aspects of Mathematics, vol. E31 (Friedr. Vieweg & Sohn, Braunschweig, 1997).Google Scholar
Illusie, L., Complexe cotangent et déformations. I, Lecture Notes in Mathematics, vol. 239 (Springer, Berlin, 1971).Google Scholar
Kawakita, M., Inversion of adjunction on log canonicity, Invent. Math. 167 (2007), 129–133.CrossRefGoogle Scholar
Kollár, J., Flatness criteria, J. Algebra 175 (1995), 715–727.Google Scholar
Kollár, J., Moduli of varieties of general type, Preprint (2010), arXiv:1008.0621.Google Scholar
Kollár, J., Singularities of the Minimal Model Program, Cambridge Tracts in Mathematics, vol. 200 (Cambridge University Press, Cambridge, 2013).Google Scholar
Kovács, S. J., Young person’s guide to moduli of higher dimensional varieties, in Algebraic Geometry—Seattle 2005. Part 2, Proceedings of Symposia in Pure Mathematics, vol. 80 (American Mathematical Society, Providence, RI, 2009), 711–743.Google Scholar
Lee, Y., A compactification of a family of determinantal Godeaux surfaces, Trans. Amer. Math. Soc. 352 (2000), 5013–5023.CrossRefGoogle Scholar
Liu, W., Stable degenerations of surfaces isogenous to a product ii, Trans. Amer. Math. Soc. 364 (2012), 2411–2427.CrossRefGoogle Scholar
Lurie, J., Derived algebraic geometry. PhD thesis, M.I.T. (2004), http://www.dspace.mit.edu/handle/1721.1/30144.Google Scholar
Lurie, J., Higher topos theory, Annals of Mathematics Studies, vol. 170 (Princeton University Press, Princeton, NJ, 2009).Google Scholar
Lurie, J., Moduli problems for ring spectra (2010), http://math.harvard.edu/~lurie.Google Scholar
Lurie, J., Higher algebra (2011), http://math.harvard.edu/~lurie.Google Scholar
Matsumura, H., Commutative algebra, Mathematics Lecture Note Series, vol. 56, second edition (Benjamin/Cummings, Reading, MA, 1980).Google Scholar
Matsusaka, T. and Mumford, D., Two fundamental theorems on deformations of polarized varieties, Amer. J. Math. 86 (1964), 668–684.CrossRefGoogle Scholar
van Opstall, M. A., Moduli of products of curves, Arch. Math. (Basel) 84 (2005), 148–154.Google Scholar
van Opstall, M., Stable degenerations of surfaces isogenous to a product of curves, Proc. Amer. Math. Soc. 134 (2006), 2801–2806.CrossRefGoogle Scholar
Neeman, A., The Grothendieck duality theorem via Bousfield’s techniques and Brown representability, J. Amer. Math. Soc. 9 (1996), 205–236.Google Scholar
Quillen, D., On the (co-) homology of commutative rings, in Applications of Categorical Algebra, New York, 1968, Proceedings of Symposia in Pure Mathematics, Vol. XVII (American Mathematical Society, Providence, RI, 1970), 65–87.Google Scholar
Rollenske, S., Compact moduli for certain Kodaira fibrations, Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 9 (2010), 851–874.Google Scholar
Uhlenbeck, K. and Yau, S.-T., On the existence of Hermitian–Yang–Mills connections in stable vector bundles, Comm. Pure Appl. Math. 39(S, suppl.) (1986), S257–S293; Frontiers of the Mathematical Sciences: 1985 (New York, 1985).Google Scholar
Vakil, R., Murphy’s law in algebraic geometry: badly-behaved deformation spaces, Invent. Math. 164 (2006), 569–590.Google Scholar
Viehweg, E., Quasi-projective moduli for polarized manifolds, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], vol. 30 (Springer, Berlin, 1995).Google Scholar
Yau, S. T., On the Ricci curvature of a compact Kähler manifold and the complex Monge–Ampère equation. I, Comm. Pure Appl. Math. 31 (1978), 339–411.Google Scholar