Hostname: page-component-8448b6f56d-sxzjt Total loading time: 0 Render date: 2024-04-23T14:08:04.569Z Has data issue: false hasContentIssue false
  • English
  • Français

Mixing in a vortex breakdown flow

Published online by Cambridge University Press:  14 August 2013

P. Meunier  and
K. Hourigan
P. Meunier*
Affiliation:
IRPHE UMR7342, CNRS, Aix Marseille Université, Centrale Marseille 13013, Marseille, France Division of Biological Engineering, Monash University, Melbourne, Victoria 3800, Australia
K. Hourigan
Affiliation:
Division of Biological Engineering, Monash University, Melbourne, Victoria 3800, Australia Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, Victoria 3800, Australia
*
†Email address for correspondence: meunier@irphe.univ-mrs.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we present experimental and theoretical results on the mixing inside a cylinder with a rotating lid. The helical flow that is created by the rotation of the disc is well known to exhibit a vortex breakdown bubble over a finite range of Reynolds numbers. The mixing properties of the flow are analysed quantitatively by measuring the exponential decay of the variance as a function of time. This homogenization time is extremely sensitive to the asymmetries of the flow, which are introduced by tilting the rotating or the stationary disc and accurately measured using particle image velocimetry (PIV). In the absence of vortex breakdown, the homogenization time is strongly decreased (by a factor of 10) with only a moderate tilt angle of the rotating lid (of the order of 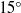$1{5}^{\circ } $). This phenomenon can be explained by the presence of small radial jets at the periphery which create a strong convective mixing. A simple model of exchange flow between the periphery and the bulk correctly predicts the scaling laws for the homogenization time. In the presence of vortex breakdown, the scalar is trapped inside the vortex breakdown bubble, and thus increases substantially the time needed for homogenization. Curiously, the tilt of the rotating lid has a weak effect on the mixing, but a small tilt of the stationary disc (of the order of 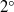${2}^{\circ } $) strongly decreases (by a factor of 10) the homogenization time. Even more surprising is that the homogenization time diverges when the size of the bubble vanishes. All of these features are recovered by applying the Melnikov theory to calculate the volume of the lobes that exit the bubble. It is the first time that this technique has been applied to a three-dimensional stationary flow with a non-axisymmetric perturbation and compared with experimental results, although it has been applied often to two-dimensional flows with a periodic perturbation.

JFM classification

Mixing: Chaotic advection Flow Control: Mixing enhancement Vortex Flows: Vortex breakdown
Type
Papers
Information
Journal of Fluid Mechanics , Volume 731 , 25 September 2013 , pp. 195 - 222
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonsen, T. M., Fan, Z., Ott, E. & Garcia-Lopez, E. 1996 The role of chaotic orbits in the determination of power spectra of passive scalars. Phys. Fluids 8 (11), 3094–3104.Google Scholar
Batchelor, G. K. 1959 Small-scale variation of convected quantities like temperature in a turbulent fluid. Part 1. General discussion and the case of small conductivity. J. Fluid Mech. 5, 113–133.Google Scholar
Benjamin, T. B. 1962 Theory of the vortex breakdown phenomenon. J. Fluid Mech. 14, 593–629.Google Scholar
Brons, M., Shen, W. Z., Sorensen, J. N. & Zhu, W. J. 2007 The influence of imperfections on the flow structure of steady vortex breakdown bubbles. J. Fluid Mech. 578, 453–466.Google Scholar
Brons, M., Thompson, M. & Hourigan, K. 2009 Dye visualization near a three-dimensional stagnation point: application to the vortex breakdown bubble. J. Fluid Mech. 622, 177–194.Google Scholar
Burggraf, O. R. & Foster, M. R. 1977 Continuation or breakdown in tornado like vortices. J. Fluid Mech. 80, 685–703.Google Scholar
Duplat, J. & Villermaux, E. 2008 Mixing by random stirring in confined mixtures. J. Fluid Mech. 617, 51–86.Google Scholar
Dusting, J., Sheridan, J. & Hourigan, K. 2006 A fluid dynamics approach to bioreactor design for cell and tissue culture. Biotechnol. Bioengng 94, 1196–1208.CrossRefGoogle ScholarPubMed
Escudier, M. P. 1984 Observations of the flow produced in a cylindrical container by a rotating endwall. Exp. Fluids 2, 189–196.Google Scholar
Escudier, M. P. 1988 Vortex breakdown: observations and explanations. Prog. Aerosp. Sci. 25, 189–229.Google Scholar
Faler, J. H. & Leibovich, S. 1978 An experimental map of the internal structure of a vortex breakdown. J. Fluid Mech. 86, 313–335.Google Scholar
Fountain, G. O., Khakar, D. V. & Ottino, J. M. 1998 Visualization of three-dimensional chaos. J. Fluid Mech. 281, 683–686.Google ScholarPubMed
Gallaire, F., Ruith, M., Meiburg, E. & Chomaz, J. M. 2006 Spiral vortex breakdown as a global mode. J. Fluid Mech. 549, 71–80.Google Scholar
Gelfgat, A. Y., Bar-Yoseph, P. Z. & Solan, A. 1996 Stability of confined swirling flow with and without vortex breakdown. J. Fluid Mech. 311, 1–36.Google Scholar
Gelfgat, A. Y., Bar-Yoseph, P. Z. & Solan, A. 2001 Three-dimensional instability of axisymmetric flow in a rotating lid-cylinder enclosure. J. Fluid Mech. 438, 363–377.Google Scholar
Gouillart, E., Kuncio, N., Dauchot, O., Dubrulle, B., Roux, S. & Thiffeault, J.-L. 2007 Walls inhibit chaotic mixing. Phys. Rev. Lett. 99, 114501.Google Scholar
Gruendler, J. 1985 The existence of homoclinic orbits and the method of Melnikov for systems in ${R}^{n} $ . SIAM J. Math. Anal. 16 (5), 907–931.CrossRefGoogle Scholar
Guckenheimer, J. & Holmes, P. 1983 Non-Linear Oscillations, Dynamical Systems and Bifurcations of Vector Fields. Springer.Google Scholar
Gupta, A. K., Lilley, D. G. & Syred, N. 1984 Swirl Flows. Abacus.Google Scholar
Hall, M. G. 1972 Vortex breakdown. Annu. Rev. Fluid Mech. 4, 195–218.CrossRefGoogle Scholar
Harvey, J. K. 1962 Some observations of the vortex breakdown phenomenon. J. Fluid Mech. 14, 585–592.Google Scholar
Haynes, P. H. & Vanneste, J. 2005 What controls the decay of passive scalars in smooth flows? Phys. Fluids 17, 097103.Google Scholar
Hindmarsh, A. C., Brown, P. N., Grant, K. E., Lee, S. L., Serban, R., Schumaker, D. E. & Woodward, C. S. 2005 Suite of nonlinear and differential/algebraic equations solvers. ACM Trans. Math. Softw. 31 (3), 363–396.Google Scholar
Holmes, P. 1984 Contemporary mathematics. Phys. Fluids 28, 393–403.Google Scholar
Ismadi, M. P., Meunier, P., Fouras, A. & Hourigan, K. 2011 Experimental control of vortex breakdown by density effects. Phys. Fluids 23, 034104.Google Scholar
Kalda, J. 2000 Simple model of intermittent passive scalar turbulence. Phys. Rev. Lett. 84 (3), 471–474.CrossRefGoogle ScholarPubMed
Leibovich, S. 1978 The structure of vortex breakdown. Annu. Rev. Fluid Mech. 10, 221–246.Google Scholar
Lopez, J. M. 2006 Rotating and modulated rotating waves in transitions of an enclosed swirling flow. J. Fluid Mech. 553, 323–346.Google Scholar
Lopez, J. M. 2012 Three-dimensional swirling flows in a tall cylinder driven by a rotating endwall. Phys. Fluids 24, 014101.Google Scholar
Lopez, J. M. & Perry, A. D. 1992 Axisymmetric vortex breakdown. Part 3. Onset of periodic flow and chaotic advection. J. Fluid Mech. 234, 449–471.CrossRefGoogle Scholar
Lowson, M. V. & Riley, A. J. 1995 Vortex breakdown control by delta wing geometry. J. Aircraft 32 (4), 832–838.Google Scholar
Meliga, P., Gallaire, F. & Chomaz, J. M. 2012 A weakly nonlinear mechanism for mode selection in swirling jets. J. Fluid Mech. 699, 216–262.Google Scholar
Meunier, P. & Leweke, T. 2003 Analysis and optimization of the error caused by high velocity gradients in PIV. Exp. Fluids 35, 408–421.Google Scholar
Meunier, P. & Villermaux, E. 2010 The diffusive strip method for scalar mixing in two dimensions. J. Fluid Mech. 662, 134–172.CrossRefGoogle Scholar
Pierrehumbert, R. T. 1994 Tacer structure in the large-eddy dominated regime. Chaos Solitons Fractals 4, 1111–1116.Google Scholar
Rom-Kedar, V., Leonard, A. & Wiggins, S. 1990 An analytical study of transport, mixing and chaos in an unsteady vortical flow. J. Fluid Mech. 214, 347–394.Google Scholar
Ronnenberg, B. 1977 Ein selbstjustierendes 3-komponenten-LDA nach dem Vergleighstrahlverfaren, angewendt für Untersuchungen in einer stationaren zylindersymmetrischen Drehströmung mit einem Rühckströmgebiet. Technical Report Bericht 20, Max-Planck-Institut für Strömungsforschung, Göttingen.Google Scholar
Rotunno, R. 2012 The fluid dynamics of tornadoes. Annu. Rev. Fluid Mech. 45, 59–84.CrossRefGoogle Scholar
Ruith, M. R., Chen, P., Meiburg, E. & Maxworthy, T. 2003 Three-dimensional vortex breakdown in swirling jets and wakes: direct numerical simulation. J. Fluid Mech. 486, 331–378.Google Scholar
Sarpkaya, T. 1971 On stationary and travelling vortex breakdowns. J. Fluid Mech. 45, 545–559.Google Scholar
Sorensen, J. N., Naumov, I. V. & Okulov, V. L. 2011 Multiple helical modes of vortex breakdown. J. Fluid Mech. 683, 430–441.Google Scholar
Sotiropoulos, F., Ventikos, Y. & Lackey, T. C. 2001 Chaotic advection in three-dimensional stationary vortex-breakdown bubbles: Sil’nikov’s chaos and the devil’s staircase. J. Fluid Mech. 444, 257–297.Google Scholar
Sotiropoulos, F., Webster, D. R. & Lackey, T. C. 2002 Experiments on Lagrangian transport in steady vortex-breakdown bubbles in a confined swirling flow. J. Fluid Mech. 466, 215–248.Google Scholar
Spohn, A., Mory, M. & Hopfinger, E. J. 1998 Experiments on vortex breakdown in a confined flow generated by a rotating disc. J. Fluid Mech. 370, 73–99.Google Scholar
Thiffeault, J. L., Doering, C. R. & Gibbon, J. D. 2004 A bound on mixing efficiency for the advection diffusion equation. J. Fluid Mech. 521, 105–114.Google Scholar
Thompson, M. C. & Hourigan, K. 2003 The sensitivity of steady vortex breakdown bubbles in confined cylinder flows to rotating lid misalignment. J. Fluid Mech. 496, 129–138.Google Scholar
Thouas, G. A., Sheridan, J. & Hourigan, K. 2007 A bioreactor model of mouse tumor progression. J. Biomed. Biotechnol. 9, 32754.Google Scholar
Toussaint, V., Carrière, P. & Raynal, F. 1995 A numerical Eulerian approach to mixing by chaotic advection. Phys. Fluids 7, 2587–2600.Google Scholar
Toussaint, V., Carrière, P., Scott, J. & Gence, J. N. 2000 Spectral decay of a passive scalar in chaotic mixing. Phys. Fluids 12 (11), 2834–2844.Google Scholar
Vogel, H. U. 1968 Experimentelle Ergebnisse über die laminare Strömung in einem zylindrischen Gehaüse mit darin rotierender Scheibe. Technical Report Bericht 6, Max-Planck-Institut für Strömungsforschung, Göttingen.Google Scholar
Wang, S. & Rusak, Z. 1997 The dynamics of a swirling flow in a pipe and transition to axisymmetric vortex breakdown. J. Fluid Mech. 340, 177–223.Google Scholar
Warhaft, Z. 2000 Passive scalars in turbulent flows. Annu. Rev. Fluid Mech. 32, 203–240.Google Scholar
Wentz, W. H. & Kohlman, D. L. 1971 Vortex breakdown on slender sharp-edged wings. J. Aircraft 8 (3), 156–161.Google Scholar
Wiggins, S. 2003 Introduction to Applied Nonlinear Dynamical Systems and Chaos. Springer.Google Scholar