Hostname: page-component-76fb5796d-dfsvx Total loading time: 0 Render date: 2024-04-25T09:40:24.700Z Has data issue: false hasContentIssue false
  • English
  • Français

ONE-POINT EXTENSIONS AND LOCAL TOPOLOGICAL PROPERTIES

Part of: Fairly general properties

Published online by Cambridge University Press:  02 August 2012

M. R. KOUSHESH
M. R. KOUSHESH*
Affiliation:
Department of Mathematical Sciences, Isfahan University of Technology, Isfahan 84156-83111, Iran School of Mathematics, Institute for Research in Fundamental Sciences (IPM), P.O. Box: 19395-5746, Tehran, Iran (email: koushesh@cc.iut.ac.ir)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A space 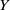$Y$ is called an extension of a space 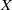$X$ if 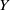$Y$ contains 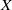$X$ as a dense subspace. An extension 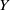$Y$ of 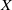$X$ is called a one-point extension of 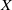$X$ if 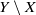$Y\setminus X$ is a singleton. P. Alexandroff proved that any locally compact non-compact Hausdorff space 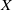$X$ has a one-point compact Hausdorff extension, called the one-point compactification of 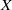$X$. Motivated by this, Mrówka and Tsai [‘On local topological properties. II’, Bull. Acad. Polon. Sci. Sér. Sci. Math. Astronom. 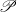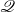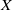Phys.19 (1971), 1035–1040] posed the following more general question: For what pairs of topological properties ${\mathscr P}$ and ${\mathscr Q}$ does a locally-${\mathscr P}$ space $X$ having 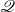${\mathscr Q}$ possess a one-point extension having both 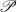${\mathscr P}$ and 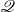${\mathscr Q}$? Here, we provide an answer to this old question.

Keywords

Stone–Čech compactificationone-point extensionone-point compactificationMrówka’s condition W

MSC classification

Secondary: 54D35: Extensions of spaces (compactifications, supercompactifications, completions, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 88 , Issue 1 , August 2013 , pp. 12 - 16
Copyright
Copyright © 2012 Australian Mathematical Publishing Association Inc. 

References

[1]Burke, D. K., ‘Covering properties’, in: Handbook of Set-Theoretic Topology, (eds. Kunen, K. & Vaughan, J. E.) (Elsevier, Amsterdam, 1984), pp. 347–422.CrossRefGoogle Scholar
[2]Engelking, R., General Topology, 2nd edn (Heldermann, Berlin, 1989).Google Scholar
[3]Engelking, R. & Mrówka, S., ‘On $E$-compact spaces’, Bull. Acad. Polon. Sci. Sér. Sci. Math. Astr. Phys. 6 (1958), 429–436.Google Scholar
[4]Koushesh, M. R., ‘Compactification-like extensions’, Dissertationes Math. (Rozprawy Mat.) 476 (2011), 88pp.Google Scholar
[5]Koushesh, M. R., ‘The partially ordered set of one-point extensions’, Topology Appl. 158 (2011), 509–532.CrossRefGoogle Scholar
[6]Koushesh, M. R., ‘A pseudocompactification’, Topology Appl. 158 (2011), 2191–2197.CrossRefGoogle Scholar
[7]Mack, J., Rayburn, M. & Woods, R. G., ‘Local topological properties and one-point extensions’, Canad. J. Math. 24 (1972), 338–348.CrossRefGoogle Scholar
[8]Mack, J., Rayburn, M. & Woods, R. G., ‘Lattices of topological extensions’, Trans. Amer. Math. Soc. 189 (1974), 163–174.CrossRefGoogle Scholar
[9]Marin, F. L., ‘A note on $E$-compact spaces’, Fund. Math. 76 (1972), 195–206.CrossRefGoogle Scholar
[10]Mrówka, S., ‘On local topological properties’, Bull. Acad. Polon. Sci. 5 (1957), 951–956.Google Scholar
[11]Mrówka, S., ‘Further results on $E$-compact spaces. I’, Acta Math. 120 (1968), 161–185.CrossRefGoogle Scholar
[12]Mrówka, S. & Tsai, J. H., ‘On local topological properties. II’, Bull. Acad. Polon. Sci. Sér. Sci. Math. Astronom. Phys. 19 (1971), 1035–1040.Google Scholar
[13]Stephenson, R. M., ‘Initially $\kappa $-compact and related spaces’, in: Handbook of Set-Theoretic Topology, (eds. Kunen, K. & Vaughan, J. E.) (Elsevier, Amsterdam, 1984), pp. 603–632.CrossRefGoogle Scholar
[14]Tsai, J. H., ‘More on local topological properties’, Bull. Acad. Polon. Sci. Sér. Sci. Math. Astronom. Phys. 22 (1974), 49–51.Google Scholar