Hostname: page-component-8448b6f56d-wq2xx Total loading time: 0 Render date: 2024-04-25T04:11:42.409Z Has data issue: false hasContentIssue false
  • English
  • Français

Cohomological and projective dimensions

Part of: (Co)homology theory Commutative algebra: Homological methods

Published online by Cambridge University Press:  01 May 2013

Matteo Varbaro
Matteo Varbaro*
Affiliation:
Dipartimento di Matematica, Università degli Studi di Genova, Italy email varbaro@dima.unige.it
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

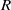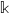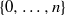Let $\mathfrak{a}$ be a homogeneous ideal of a polynomial ring $R$ in $n$ variables over a field $\mathbb{k}$. Assume that $\mathrm{depth} (R/ \mathfrak{a})\geq t$, where $t$ is some number in $\{ 0, \ldots , n\} $. A result of Peskine and Szpiro says that if 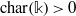$\mathrm{char} (\mathbb{k})\gt 0$, then the local cohomology modules 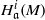${ H}_{\mathfrak{a}}^{i} (M)$ vanish for all 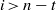$i\gt n- t$ and all $R$-modules 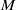$M$. In characteristic 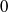$0$, there are counterexamples to this for all 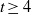$t\geq 4$. On the other hand, when 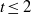$t\leq 2$, by exploiting classical results of Grothendieck, Lichtenbaum, Hartshorne and Ogus it is not difficult to extend the result to any characteristic. In this paper we settle the remaining case; specifically, we show that if 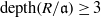$\mathrm{depth} (R/ \mathfrak{a})\geq 3$, then the local cohomology modules 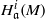${ H}_{\mathfrak{a}}^{i} (M)$ vanish for all 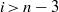$i\gt n- 3$ and all 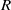$R$-modules 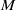$M$, whatever the characteristic of 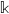$\mathbb{k}$ is.

Keywords

cohomological dimensionprojective dimensiondepthperfect ideals

MSC classification

Secondary: 13D45: Local cohomology 14F17: Vanishing theorems
Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 7 , July 2013 , pp. 1203 - 1210
Copyright
© The Author(s) 2013 

References

Arapura, D., Algebraic geometry over the complex numbers (Springer, New York, 2012).Google Scholar
Bourbaki, N., Éléments de mathématique: Algébre commutative, Chapitres 8 & 9 (Springer, Berlin, 2008).Google Scholar
Bruns, W. and Schwänzl, R., The number of equations defining a determinantal variety, Bull. Lond. Math. Soc. 22 (1990), 439–445.Google Scholar
Bruns, W. and Vetter, U., Determinantal rings, Lecture Notes in Mathematics, vol. 1327 (Springer, Berlin, 1980).Google Scholar
Buchsbaum, D. A. and Eisenbud, D., What makes a complex exact? J. Algebra 25 (1973), 259–268.CrossRefGoogle Scholar
Faltings, G., Über lokale Kohomologiegruppen hoher Ordnung, J. Reine Angew. Math. 313 (1980), 43–51.Google Scholar
Grayson, D. R. and Stillman, M. E., Macaulay 2, a software system for research in algebraic geometry, http://www.math.uiuc.edu/Macaulay2.Google Scholar
Grothendieck, A., Local cohomology: a seminar given by A. Grothendieck, Harvard University, 1961, Lecture Notes in Mathematics, vol. 41, ed. Hartshorne, R. (Springer, Berlin, 1967).Google Scholar
Gunning, R. C. and Rossi, H., Analytic functions of several complex variables (Prentice Hall, Englewood Cliffs, 1965).Google Scholar
Hartshorne, R., Complete intersection and connectedness, Amer. J. Math. 84 (1962), 497–508.Google Scholar
Hartshorne, R., Cohomological dimension of algebraic varieties, Ann. of Math. (2) 88 (1968), 403–450.CrossRefGoogle Scholar
Hartshorne, R., Ample subvarieties of algebraic varieties, Lecture Notes in Mathematics, vol. 156 (Springer, New York, 1970).Google Scholar
Hartshorne, R., On the de Rham cohomology of algebraic varieties, Publ. Math. Inst. Hautes Études Sci. 45 (1975), 5–99.Google Scholar
Hartshorne, R. and Speiser, R., Local cohomological dimension in characteristic $p$, Ann. of Math. (2) 105 (1977), 45–79.Google Scholar
Huneke, C. and Lyubeznik, G., On the vanishing of local cohomology modules, Invent. Math. 102 (1990), 73–93.Google Scholar
Kunz, E., Characterization of regular local rings of characteristic $p$, Amer. J. Math. 91 (1969), 772–784.Google Scholar
Lyubeznik, G., On the local cohomology modules ${ H}_{\mathfrak{U}}^{i} (R)$ for ideals $\mathfrak{U}$ generated by an $R$-sequence, in Complete intersection, Lecture Notes in Mathematics, vol. 1092 (Springer, New York, 1984), 214–220.Google Scholar
Lyubeznik, G., Finiteness properties of local cohomology modules, Invent. Math. 113 (1993), 41–55.Google Scholar
Lyubeznik, G., On the vanishing of local cohomology in characteristic $p\gt 0$, Compositio Math. 142 (2006), 207–221.Google Scholar
Matsumura, H., Commutative ring theory, Cambridge Studies in Advanced Mathematics, vol. 8 (Cambridge University Press, Cambridge, 1980).Google Scholar
Ogus, A., Local cohomological dimension, Ann. of Math. (2) 98 (1973), 327–365.Google Scholar
Peskine, C. and Szpiro, L., Dimension projective finie et cohomologie locale, Publ. Math. Inst. Hautes Études Sci. 42 (1973), 47–119.Google Scholar
Serre, J. P., Geometrie algebrique et geometrie analytique, Ann. Inst. Fourier 6 (1956), 1–42.CrossRefGoogle Scholar
Singh, A. K. and Walther, U., On the arithmetic rank of certain Segre products, Contemp. Math. 390 (2005), 147–155.Google Scholar
Varbaro, M., On the arithmetical rank of certain Segre embeddings, Trans. Amer. Math. Soc. 364 (2012), 5091–5109.Google Scholar