No CrossRef data available.
Article contents
Families of canonically polarized manifolds over log Fano varieties
Published online by Cambridge University Press: 26 March 2013
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let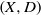 
$(X,D)$ be a dlt pair, where 
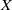$X$ is a normal projective variety. We show that any smooth family of canonically polarized varieties over 
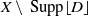$X\setminus \,{\rm Supp}\lfloor D \rfloor $ is isotrivial if the divisor 
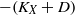$-(K_X+D)$ is ample. This result extends results of Viehweg–Zuo and Kebekus–Kovács. To prove this result we show that any extremal ray of the moving cone is generated by a family of curves, and these curves are contracted after a certain run of the minimal model program. In the log Fano case, this generalizes a theorem by Araujo from the klt to the dlt case. In order to run the minimal model program, we have to switch to a 
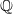$\mathbb Q$-factorialization of 
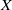$X$. As 
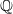$\mathbb Q$-factorializations are generally not unique, we use flops to pass from one 
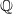$\mathbb Q$-factorialization to another, proving the existence of a 
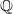$\mathbb Q$-factorialization suitable for our purposes.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © 2013 The Author(s)
References
[Ara10]Araujo, C., The cone of pseudo-effective divisors of log varieties after Batyrev, Math. Z. 264 (2010), 179–193.CrossRefGoogle Scholar
[Bar08]Barkowski, S., The cone of moving curves of a smooth Fano three- or fourfold. PhD thesis, Mathematisches Institut der Universität zu Köln, Kölner Universitäts-Publikations-Server (KUPS) (2008), urn:nbn:de:hbz:38 25085.Google Scholar
[Bar10]Barkowski, S., The cone of moving curves of a smooth Fano three- or fourfold, Manuscripta Math. 131 (2010), 305–322.Google Scholar
[BCHM10]Birkar, C., Cascini, P., Hacon, C. D. and McKernan, J., Existence of minimal models for varieties of log general type, J. Amer. Math. Soc. 23 (2010), 405–468.CrossRefGoogle Scholar
[Bir10]Birkar, C., On existence of log minimal models, Composito. Math. 146 (2010), 919–928.Google Scholar
[BDPP04]Boucksom, S., Demailly, J.-P., Paun, M. and Peternell, T., The pseudo-effective cone of a compact Kähler manifold and varieties of negative Kodaira dimension, J. Algebraic Geom., to appear, arXiv:math/0405285v1.Google Scholar
[Deb01]Debarre, O., Higher-dimensional algebraic geometry, Universitext (Springer, New York, 2001).Google Scholar
[GKKP11]Greb, D., Kebekus, S., Kovács, S. and Peternell, T., Differential forms on log canonical spaces, Publ. Math. Inst. Hautes Études Sci. 114 (2011), 87–169 DOI:10.1007/s10240-011-0036-0. An extended version with additional graphics is available as arXiv:1003.2913.CrossRefGoogle Scholar
[HK00]Hu, Y. and Keel, S., Mori dream spaces and GIT, Michigan Math. J. 48 (2000), 331–348. Dedicated to William Fulton on the occasion of his 60th birthday.CrossRefGoogle Scholar
[Keb11]Kebekus, S., Differential forms on singular spaces, the minimal model program, and hyperbolicity of moduli stacks, in Handbook of Moduli in honour of David Mumford, eds G. Farkas and I. Morrison (International Press), to appear, arXiv:1107.4239v1.Google Scholar
[KK08a]Kebekus, S. and Kovács, S. J., Families of canonically polarized varieties over surfaces, Invent. Math. 172 (2008), 657–682.Google Scholar
[KK08b]Kebekus, S. and Kovács, S. J., Families of varieties of general type over compact bases, Adv. Math. 218 (2008), 649–652.CrossRefGoogle Scholar
[KK10]Kebekus, S. and Kovács, S., The structure of surfaces and threefolds mapping to the moduli stack of canonically polarized varieties, Duke Math. J. 155 (2010), 1–33.Google Scholar
[KM98]Kollár, J. and Mori, S., Birational geometry of algebraic varieties, Cambridge Tracts in Mathematics, vol. 134 (Cambridge University Press, Cambridge, 1998), with the collaboration of C. H. Clemens and A. Corti, translated from the 1998 Japanese original.CrossRefGoogle Scholar
[Kov00]Kovács, S. J., Algebraic hyperbolicity of fine moduli spaces, J. Algebraic Geom. 9 (2000), 165–174.Google Scholar
[Kov09]Kovács, S. J., Subvarieties of moduli stacks of canonically polarized varieties: generalizations of Shafarevich’s conjecture, in Algebraic geometry—Seattle 2005. Part 2, Proceedings of Symposium in Pure Mathematics, vol. 80 (Amer. Math. Soc, Providence, RI, 2009), 685–709.Google Scholar
[Laz04]Lazarsfeld, R., Positivity in algebraic geometry. II, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics, vol. 49 (Springer, Berlin, 2004).Google Scholar
[Mat02]Matsuki, K., Introduction to the Mori program, Universitext (Springer, New York, 2002).Google Scholar
[Sha94]Shafarevich, I. R., Basic algebraic geometry: varieties in projective space. 1, second edition (Springer, Berlin, 1994), translated from the 1988 Russian edition and with notes by Miles Reid.Google Scholar
[Vie95]Viehweg, E., Quasi-projective moduli for polarized manifolds, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics, vol. 30 (Springer, Berlin, 1995).Google Scholar
[Vie01]Viehweg, E., Positivity of direct image sheaves and applications to families of higher dimensional manifolds, in Vanishing Theorems and Effective Results in Algebraic Geometry (Trieste, 2000), ICTP Lectures Notes, vol. 6 (Abdus Salam Int. Cent. Theoret. Phys., Trieste, 2001), pp. 249–284. Available on the ICTP web site, http://publications.ictp.it/lns/vol6.html.Google Scholar
[VZ02]Viehweg, E. and Zuo, K., Base spaces of non-isotrivial families of smooth minimal models, in Complex geometry (Göttingen, 2000) (Springer, Berlin, 2002), 279–328.CrossRefGoogle Scholar
You have
Access