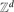Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Aleksandrowicz, Gadi
and
Barequet, Gill
2014.
The growth rate of high-dimensional tree polycubes.
European Journal of Combinatorics,
Vol. 35,
Issue. ,
p.
32.
Fitzner, Robert
and
van der Hofstad, Remco
2021.
NoBLE for Lattice Trees and Lattice Animals.
Journal of Statistical Physics,
Vol. 185,
Issue. 2,
Georgakopoulos, Agelos
and
Panagiotis, Christoforos
2023.
On the exponential growth rates of lattice animals and interfaces.
Combinatorics, Probability and Computing,
Vol. 32,
Issue. 6,
p.
912.
Slade, Gordon
2023.
Self‐avoiding walk on the hypercube.
Random Structures & Algorithms,
Vol. 62,
Issue. 3,
p.
689.
Kawamoto, Noe
and
Sakai, Akira
2024.
Spread-out limit of the critical points for lattice trees and lattice animals in dimensions .
Combinatorics, Probability and Computing,
Vol. 33,
Issue. 2,
p.
238.