Article contents
ON A CLASS OF MONOMIAL IDEALS
Published online by Cambridge University Press: 28 January 2013
Abstract
Let 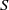 $S$ be a polynomial ring over a field
$S$ be a polynomial ring over a field 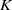 $K$ and let
$K$ and let 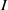 $I$ be a monomial ideal of
$I$ be a monomial ideal of 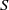 $S$. We say that
$S$. We say that 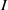 $I$ is MHC (that is,
$I$ is MHC (that is, 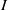 $I$ satisfies the maximal height condition for the associated primes of
$I$ satisfies the maximal height condition for the associated primes of 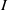 $I$) if there exists a prime ideal
$I$) if there exists a prime ideal 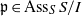 $\mathfrak{p}\in {\mathrm{Ass} }_{S} \hspace{0.167em} S/ I$ for which
$\mathfrak{p}\in {\mathrm{Ass} }_{S} \hspace{0.167em} S/ I$ for which 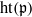 $\mathrm{ht} (\mathfrak{p})$ equals the number of indeterminates that appear in the minimal set of monomials generating
$\mathrm{ht} (\mathfrak{p})$ equals the number of indeterminates that appear in the minimal set of monomials generating 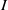 $I$. Let
$I$. Let 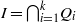 $I= { \mathop{\bigcap }\nolimits}_{i= 1}^{k} {Q}_{i} $ be the irreducible decomposition of
$I= { \mathop{\bigcap }\nolimits}_{i= 1}^{k} {Q}_{i} $ be the irreducible decomposition of 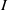 $I$ and let
$I$ and let 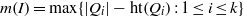 $m(I)= \max \{ \vert Q_{i}\vert - \mathrm{ht} ({Q}_{i} ): 1\leq i\leq k\} $, where
$m(I)= \max \{ \vert Q_{i}\vert - \mathrm{ht} ({Q}_{i} ): 1\leq i\leq k\} $, where 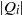 $\vert {Q}_{i} \vert $ denotes the total degree of
$\vert {Q}_{i} \vert $ denotes the total degree of 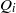 ${Q}_{i} $. Then it can be seen that when
${Q}_{i} $. Then it can be seen that when 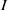 $I$ is primary,
$I$ is primary, 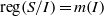 $\mathrm{reg} (S/ I)= m(I)$. In this paper we improve this result and show that whenever
$\mathrm{reg} (S/ I)= m(I)$. In this paper we improve this result and show that whenever 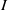 $I$ is MHC, then
$I$ is MHC, then 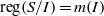 $\mathrm{reg} (S/ I)= m(I)$ provided
$\mathrm{reg} (S/ I)= m(I)$ provided 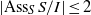 $\vert {\mathrm{Ass} }_{S} \hspace{0.167em} S/ I\vert \leq 2$. We also prove that
$\vert {\mathrm{Ass} }_{S} \hspace{0.167em} S/ I\vert \leq 2$. We also prove that 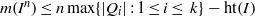 $m({I}^{n} )\leq n\max \{ \vert Q_{i}\vert : 1\leq i\leq ~k\} - \mathrm{ht} (I)$, for all
$m({I}^{n} )\leq n\max \{ \vert Q_{i}\vert : 1\leq i\leq ~k\} - \mathrm{ht} (I)$, for all 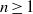 $n\geq 1$. In addition we show that if
$n\geq 1$. In addition we show that if 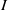 $I$ is MHC and
$I$ is MHC and 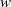 $w$ is an indeterminate which is not in the monomials generating
$w$ is an indeterminate which is not in the monomials generating 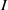 $I$, then
$I$, then 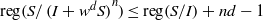 $\mathrm{reg} (S/ \mathop{(I+ {w}^{d} S)}\nolimits ^{n} )\leq \mathrm{reg} (S/ I)+ nd- 1$ for all
$\mathrm{reg} (S/ \mathop{(I+ {w}^{d} S)}\nolimits ^{n} )\leq \mathrm{reg} (S/ I)+ nd- 1$ for all 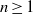 $n\geq 1$ and
$n\geq 1$ and 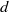 $d$ large enough. Finally, we implement an algorithm for the computation of
$d$ large enough. Finally, we implement an algorithm for the computation of 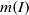 $m(I)$.
$m(I)$.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright ©2013 Australian Mathematical Publishing Association Inc.
References
- 1
- Cited by




