Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Orlicz, G. C.
Balasubramanian, S.
and
Prestridge, K. P.
2013.
Incident shock Mach number effects on Richtmyer-Meshkov mixing in a heavy gas layer.
Physics of Fluids,
Vol. 25,
Issue. 11,
Weber, Christopher R.
Haehn, Nicholas S.
Oakley, Jason G.
Rothamer, David A.
and
Bonazza, Riccardo
2014.
An experimental investigation of the turbulent mixing transition in the Richtmyer–Meshkov instability.
Journal of Fluid Mechanics,
Vol. 748,
Issue. ,
p.
457.
Reese, Daniel
Oakley, Jason
Navarro-Nunez, Alonso
Rothamer, David
Weber, Chris
and
Bonazza, Riccardo
2014.
Simultaneous concentration and velocity field measurements in a shock-accelerated mixing layer.
Experiments in Fluids,
Vol. 55,
Issue. 10,
Tritschler, V. K.
Olson, B. J.
Lele, S. K.
Hickel, S.
Hu, X. Y.
and
Adams, N. A.
2014.
On the Richtmyer–Meshkov instability evolving from a deterministic multimode planar interface.
Journal of Fluid Mechanics,
Vol. 755,
Issue. ,
p.
429.
Likhachev, Oleg A.
and
Tsiklashvili, Vladimer
2014.
Integral constraints in the study of Richtmyer-Meshkov turbulent mixing.
Physics of Fluids,
Vol. 26,
Issue. 10,
Demos, Stavros G.
Negres, Raluca A.
Raman, Rajesh N.
Feit, Michael D.
Manes, Kenneth R.
and
Rubenchik, Alexander M.
2015.
Relaxation dynamics of nanosecond laser superheated material in dielectrics.
Optica,
Vol. 2,
Issue. 8,
p.
765.
Liu, Han
and
Xiao, Zuoli
2016.
Scale-to-scale energy transfer in mixing flow induced by the Richtmyer-Meshkov instability.
Physical Review E,
Vol. 93,
Issue. 5,
Reese, Daniel
and
Weber, Christopher
2016.
Numerical investigation of 3D effects on a 2D-dominated shocked mixing layer.
Physics of Fluids,
Vol. 28,
Issue. 11,
Gao, Fujie
Zhang, Yousheng
He, Zhiwei
and
Tian, Baolin
2016.
Formula for growth rate of mixing width applied to Richtmyer-Meshkov instability.
Physics of Fluids,
Vol. 28,
Issue. 11,
Morgan, R. V.
Likhachev, O. A.
and
Jacobs, J. W.
2016.
Rarefaction-driven Rayleigh–Taylor instability. Part 1. Diffuse-interface linear stability measurements and theory.
Journal of Fluid Mechanics,
Vol. 791,
Issue. ,
p.
34.
Reese, Daniel
and
Weber, Chris
2017.
30th International Symposium on Shock Waves 2.
p.
1109.
Thornber, B.
Griffond, J.
Poujade, O.
Attal, N.
Varshochi, H.
Bigdelou, P.
Ramaprabhu, P.
Olson, B.
Greenough, J.
Zhou, Y.
Schilling, O.
Garside, K. A.
Williams, R. J. R.
Batha, C. A.
Kuchugov, P. A.
Ladonkina, M. E.
Tishkin, V. F.
Zmitrenko, N. V.
Rozanov, V. B.
and
Youngs, D. L.
2017.
Late-time growth rate, mixing, and anisotropy in the multimode narrowband Richtmyer–Meshkov instability: The θ-group collaboration.
Physics of Fluids,
Vol. 29,
Issue. 10,
Zhou, Ye
2017.
Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing. I.
Physics Reports,
Vol. 720-722,
Issue. ,
p.
1.
Subramaniam, Akshay
and
Lele, Sanjiva K.
2017.
Numerical simulation of multi-material mixing in an inclined interface Richtmyer-Meshkov instability.
Vol. 1793,
Issue. ,
p.
150006.
Mohaghar, Mohammad
Carter, John
Musci, Benjamin
Reilly, David
McFarland, Jacob
and
Ranjan, Devesh
2017.
Evaluation of turbulent mixing transition in a shock-driven variable-density flow.
Journal of Fluid Mechanics,
Vol. 831,
Issue. ,
p.
779.
Gao, Fujie
Zhang, Yousheng
He, Zhiwei
Li, Li
and
Tian, Baolin
2017.
Characteristics of turbulent mixing at late stage of the Richtmyer-Meshkov instability.
AIP Advances,
Vol. 7,
Issue. 7,
Campos, A.
and
Morgan, B.
2018.
The effect of artificial bulk viscosity in simulations of forced compressible turbulence.
Journal of Computational Physics,
Vol. 371,
Issue. ,
p.
111.
Campos, Alejandro
and
Morgan, Brandon E.
2019.
Direct numerical simulation and Reynolds-averaged Navier-Stokes modeling of the sudden viscous dissipation for multicomponent turbulence.
Physical Review E,
Vol. 99,
Issue. 6,
Campos, Alejandro
and
Morgan, Brandon E.
2019.
Self-consistent feedback mechanism for the sudden viscous dissipation of finite-Mach-number compressing turbulence.
Physical Review E,
Vol. 99,
Issue. 1,
Wong, Man Long
Livescu, Daniel
and
Lele, Sanjiva K.
2019.
High-resolution Navier-Stokes simulations of Richtmyer-Meshkov instability with reshock.
Physical Review Fluids,
Vol. 4,
Issue. 10,
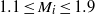 $1. 1\leq {M}_{i} \leq 1. 9$), Atwood numbers (
$1. 1\leq {M}_{i} \leq 1. 9$), Atwood numbers (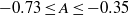 $- 0. 73\leq A\leq - 0. 35$ and
$- 0. 73\leq A\leq - 0. 35$ and 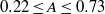 $0. 22\leq A\leq 0. 73$), adiabatic indices (
$0. 22\leq A\leq 0. 73$), adiabatic indices (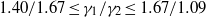 $1. 40/ 1. 67\leq {\gamma }_{1} / {\gamma }_{2} \leq 1. 67/ 1. 09$) and narrow-band perturbation spectra. The mixing layer at late times exhibits a power-law growth with an average exponent of
$1. 40/ 1. 67\leq {\gamma }_{1} / {\gamma }_{2} \leq 1. 67/ 1. 09$) and narrow-band perturbation spectra. The mixing layer at late times exhibits a power-law growth with an average exponent of 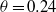 $\theta = 0. 24$.
$\theta = 0. 24$.



