Hostname: page-component-8448b6f56d-wq2xx Total loading time: 0 Render date: 2024-04-25T05:22:38.869Z Has data issue: false hasContentIssue false
  • English
  • Français

Strong stochastic stability for non-uniformly expanding maps

Published online by Cambridge University Press:  06 August 2012

JOSÉ F. ALVES  and
HELDER VILARINHO
JOSÉ F. ALVES
Affiliation:
CMUP, Rua do Campo Alegre 687, 4169-007 Porto, Portugal (email: jfalves@fc.up.pt)
HELDER VILARINHO
Affiliation:
Universidade da Beira Interior, Rua Marquês d’Ávila e Bolama, 6200-001 Covilhã, Portugal (email: helder@ubi.pt)
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider random perturbations of discrete-time dynamical systems. We give sufficient conditions for the stochastic stability of certain classes of maps, in a strong sense. This improves the main result in Alves and Araújo [Random perturbations of non-uniformly expanding maps. Astérisque 286 (2003), 25–62], where the stochastic stability in the 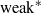$\mathrm {weak}^*$ topology was proved. Here, under slightly weaker assumptions on the random perturbations, we obtain a stronger version of stochastic stability: convergence of the density of the stationary measure to the density of the Sinai–Ruelle–Bowen (SRB) measure of the unperturbed system in the 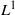$L^1$-norm. As an application of our results, we obtain strong stochastic stability for two classes of non-uniformly expanding maps. The first one is an open class of local diffeomorphisms introduced in Alves, Bonatti and Viana [SRB measures for partially hyperbolic systems whose central direction is mostly expanding. Invent. Math. 140 (2000), 351–398] and the second one is the class of Viana maps.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 33 , Issue 3 , June 2013 , pp. 647 - 692
Copyright
Copyright © 2012 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[Al00]Alves, J. F.. SRB measures for non-hyperbolic systems with multidimensional expansion. Ann. Scient. Éc. Norm. Sup., 4e série 33 (2000), 1–32.Google Scholar
[Al03]Alves, J. F.. Statistical analysis of non-uniformly expanding dynamical systems, 24th Braz. Math. Colloq., IMPA, Rio de Janeiro, 2003.Google Scholar
[Al04]Alves, J. F.. Strong statistical stability of non-uniformly expanding maps. Nonlinearity 17(4) (2004), 1193–1215.Google Scholar
[AA03]Alves, J. F. and Araújo, V.. Random perturbations of non-uniformly expanding maps. Astérisque 286 (2003), 25–62.Google Scholar
[AAV07]Alves, J. F., Araújo, V. and Vásquez, C. H.. Stochastic stability of non-uniformly hyperbolic diffeomorphisms. Stoch. Dyn. 7(3) (2007), 299–333.Google Scholar
[ABV00]Alves, J. F., Bonatti, C. and Viana, M.. SRB measures for partially hyperbolic systems whose central direction is mostly expanding. Invent. Math. 140 (2000), 351–398.CrossRefGoogle Scholar
[ALP05]Alves, J. F., Luzzatto, S. and Pinheiro, V.. Markov structures and decay of correlations for non-uniformly expanding dynamical systems. Ann. Inst. H. Poincaré Anal. Non Linéaire 22(6) (2005), 817–839.Google Scholar
[AV02]Alves, J. F. and Viana, M.. Statistical stability for robust classes of maps with non-uniform expansion. Ergod. Th. & Dynam. Sys. 22 (2002), 1–32.Google Scholar
[Ara00]Araújo, V.. Attractors and time averages for random maps. Ann. Inst. H. Poincaré Anal. Non Linéaire 17 (2000), 307–369.Google Scholar
[Arn98]Arnold, L.. Random Dynamical Systems. Springer, Berlin, 1998.Google Scholar
[Ba97]Baladi, V.. Correlation spectrum of quenched and annealed equilibrium states for random expanding maps. Commun. Math. Phys. 186 (1997), 671–700.Google Scholar
[BBM02]Baladi, V., Benedicks, M. and Maume-Deschamps, V.. Almost sure rates of mixing for i.i.d. unimodal maps. Ann. Scient. Éc. Norm. Sup., 4e série 35 (2002), 77–126.Google Scholar
[BBM10]Baladi, V., Benedicks, M. and Maume-Deschamps, V.. Correcting the proof of Theorem 3.2 in Almost sure rates of mixing for i.i.d. unimodal maps. Ann. E.N.S. (2002), arXiv:1008.5165 (2010).Google Scholar
[BKS96]Baladi, V., Kondah, A. and Schmitt, B.. Random correlations for small perturbations of expanding maps. Random Comput. Dynam. 4 (1996), 179–204.Google Scholar
[BaV96]Baladi, V. and Viana, M.. Strong stochastic stability and rate of mixing for unimodal maps. Ann. Scient. Éc. Norm. Sup., 4e série 29 (1996), 483–517.Google Scholar
[BaY93]Baladi, V. and Young, L.-S.. On the spectra of randomly perturbed expanding maps. Comm. Math. Phys 156 (1993), 355–385; Erratum, Comm. Math. Phys. 166 (1994), 219–220.Google Scholar
[BeC85]Benedicks, M. and Carleson, L.. On iterations of $1-ax^2$ on ($-1, 1$). Ann. of Math. (2) 122 (1985), 1–25.Google Scholar
[BeC91]Benedicks, M. and Carleson, L.. The dynamics of the Hénon map. Ann. of Math. (2) 133 (1991), 73–169.Google Scholar
[BeV06]Benedicks, M. and Viana, M.. Random perturbations and statistical properties of Hénon-like maps. Ann. Inst. H. Poincaré Anal. Non Linéaire 23(5) (2006), 713–752.Google Scholar
[BeY92]Benedicks, M. and Young, L.-S.. Absolutely continuous invariant measures and random perturbations for certain one-dimensional maps. Ergod. Th. & Dynam. Sys. 12 (1992), 13–37.Google Scholar
[Bo75]Bowen, R.. Equilibrium States and the Ergodic Theory of Axiom A Diffeomorphisms (Lecture Notes in Mathematics, 480). Springer, 1975.Google Scholar
[BR75]Bowen, R. and Ruelle, D.. The ergodic theory of Axiom A flows. Invent. Math. 29 (1975), 181–202.Google Scholar
[CE80]Collet, P. and Eckmann, J.. On the abundance of aperiodic behavior for maps on the interval. Comm. Math. Phys. 73 (1980), 115–160.Google Scholar
[CY05]Cowieson, W. and Young, L.-S.. SRB measures as zero-noise limits. Ergod. Th. & Dynam. Sys. 25(4) (2005), 1091–1113.CrossRefGoogle Scholar
[Ja81]Jakobson, M.. Absolutely continuous invariant measures for one parameter families of one-dimensional maps. Comm. Math. Phys. 81 (1981), 39–88.Google Scholar
[KK86]Katok, A. and Kifer, Y.. Random perturbations of transformations of an interval. J. Anal. Math. 47 (1986), 193–237.Google Scholar
[Ki86]Kifer, Y.. Ergodic Theory of Random Perturbations. Birkhäuser, Boston, Basel, 1986.CrossRefGoogle Scholar
[Ki88]Kifer, Y.. Random Perturbations of Dynamical Systems. Birkhäuser, Boston, Basel, 1988.Google Scholar
[KS69]Krzyzewski, K. and Szlenk, W.. On invariant measures for expanding differentiable mappings. Stud. Math. 33 (1969), 83–92.Google Scholar
[LQ95]Liu, P.-D. and Qian, M.. Smooth Ergodic Theory of Random Dynamical Systems. Springer, Heidelberg, 1995.Google Scholar
[Me00]Metzger, R. J.. Stochastic stability for contracting Lorenz maps and flows. Commun. Math. Phys. 212 (2000), 277–296.Google Scholar
[Oh83]Ohno, T.. Asymptotic behaviors of dynamical systems with random parameters. Publ. RIMS Kyoto Univ. 19 (1983), 83–98.Google Scholar
[Pa00]Palis, J.. A global view of dynamics and a conjecture on the denseness of finitude of attractors. Astérisque 261 (2000), 335–347.Google Scholar
[Ru76]Ruelle, D.. A measure associated with Axiom A attractors. Amer. Jour. Math. 98 (1976), 619–654.Google Scholar
[Si72]Sinai, Y.. Gibbs measures in ergodic theory. Russ. Math. Surv. 27(4) (1972), 21–69.Google Scholar
[Vi97]Viana, M.. Multidimensional non-hyperbolic attractors. Publ. Math. IHES 85 (1997), 63–96.Google Scholar
[Yo86]Young, L.-S.. Stochastic stability of hyperbolic attractors. Ergod. Th. & Dynam. Sys. 6 (1986), 311–319.CrossRefGoogle Scholar
[Yo99]Young, L.-S.. Recurrence times and rates of mixing. Israel J. Math. 110 (1999), 153–188.Google Scholar
[Yo02]Young, L.-S.. What are SRB measures, and which dynamical systems have them? J. Stat. Phys. 108(5) (2002), 733–754.CrossRefGoogle Scholar