Article contents
Extension and averaging operators for finite fields
Published online by Cambridge University Press: 30 April 2013
Abstract
In this paper we study Lp−Lr estimates of both the extension operator and the averaging operator associated with the algebraic variety S = {x ∈ 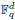 : Q(x) = 0}, where Q(x) is a non-degenerate quadratic form over the finite field
: Q(x) = 0}, where Q(x) is a non-degenerate quadratic form over the finite field 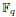 with q elements. We show that the Fourier decay estimate on S is good enough to establish the sharp averaging estimates in odd dimensions. In addition, the Fourier decay estimate enables us to simply extend the sharp L2−L4 conical extension result in
with q elements. We show that the Fourier decay estimate on S is good enough to establish the sharp averaging estimates in odd dimensions. In addition, the Fourier decay estimate enables us to simply extend the sharp L2−L4 conical extension result in 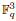 , due to Mockenhaupt and Tao, to the L2−L2(d+1)/(d−1) estimate in all odd dimensions d ≥ 3. We also establish a sharp estimate of the mapping properties of the average operators in the case when the variety S in even dimensions d ≥ 4 contains a d/2-dimensional subspace.
, due to Mockenhaupt and Tao, to the L2−L2(d+1)/(d−1) estimate in all odd dimensions d ≥ 3. We also establish a sharp estimate of the mapping properties of the average operators in the case when the variety S in even dimensions d ≥ 4 contains a d/2-dimensional subspace.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 2013
References
- 8
- Cited by




