Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-25T00:06:59.578Z Has data issue: false hasContentIssue false
  • English
  • Français

On derivations and elementary operators on C*-algebras

Part of: Fiber spaces and bundles Selfadjoint operator algebras Special classes of linear operators

Published online by Cambridge University Press:  21 March 2013

Ilja Gogić
Ilja Gogić*
Affiliation:
Department of Mathematics, University of Zagreb, Bijenička Cesta 30, Zagreb 10000, Croatia (ilja@math.hr)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A be a unital C*-algebra with the canonical (H) C*-bundle 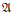over the maximal ideal space of the centre of A, and let E(A) be the set of all elementary operators on A. We consider derivations on A which lie in the completely bounded norm closure of E(A), and show that such derivations are necessarily inner in the case when each fibre of 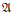is a prime C*-algebra. We also consider separable C*-algebras A for which 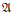is an (F) bundle. For these C*-algebras we show that the following conditions are equivalent: E(A) is closed in the operator norm; A as a Banach module over its centre is topologically finitely generated; fibres of 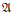have uniformly finite dimensions, and each restriction bundle of 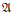over a set where its fibres are of constant dimension is of finite type as a vector bundle.

Keywords

C*-algebraderivationelementary operatoridealC*-bundlevector bundle

MSC classification

Secondary: 46L05: General theory of $C^*$-algebras 47B47: Commutators, derivations, elementary operators, etc. 46L07: Operator spaces and completely bounded maps 55R05: Fiber spaces 46L08: $C^*$-modules
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 56 , Issue 2 , June 2013 , pp. 515 - 534
Copyright
Copyright © Edinburgh Mathematical Society 2013

References

1.Akemann, C. A. and Pedersen, G. K., Central sequences and inner derivations of separable C*-algebras, Am. J. Math. 101 (1979), 1047–1061.CrossRefGoogle Scholar
2.Allen, S. D., Sinclair, A. M. and Smith, R. R., The ideal structure of the Haagerup tensor product of C*-algebras, J. Reine Angew. Math. 442 (1993), 111–148.Google Scholar
3.Ara, P. and Mathieu, M., Local multipliers of C*-algebras (Springer, 2003).CrossRefGoogle Scholar
4.Archbold, R. J., Topologies for primal ideals, J. Lond. Math. Soc. (2) 36 (1987), 524–542.CrossRefGoogle Scholar
5.Archbold, R. J. and Somerset, D. W. B., Quasi-standard C*-algebras, Math. Proc. Camb. Phil. Soc. 107 (1990), 349–360.CrossRefGoogle Scholar
6.Archbold, R. J., Kaniuth, E., Schlichting, G., Somerset, D. W. B., Ideal spaces of the Haagerup tensor product of C*-algebras, Int. J. Math. 8 (1997), 1–29.CrossRefGoogle Scholar
7.Archbold, R. J., Somerset, D. W. B. and Timoney, R. M., On the central Haagerup tensor product and completely bounded mappings of a C*-algebra, J. Funct. Analysis 226 (2005), 406–428.CrossRefGoogle Scholar
8.Archbold, R. J., Somerset, D. W. B. and Timoney, R. M., Completely bounded mappings and simplicial complex structure in the primitive ideal space of a C*-algebra, Trans. Am. Math. Soc. 361 (2009), 1397–1427.CrossRefGoogle Scholar
9.Blackadar, B., Operator algebras: theory of C*-algebras and von Neumann algebras, Encyclopaedia of Mathematical Science, Volume 122 (Springer, 2006).CrossRefGoogle Scholar
10.Blecher, D. P. and Le Merdy, C., Operator algebras and their modules (Clarendon Press, Oxford, 2004).CrossRefGoogle Scholar
11.Dixmier, J., C*-algebras (North-Holland, Amsterdam, 1977).Google Scholar
12.Dupré, M. J., Classifying Hilbert bundles, J. Funct. Analysis 15 (1974), 244–278.CrossRefGoogle Scholar
13.Dupré, M. J. and Gillette, R. M., Banach bundles, Banach modules and automor-phisms of C*-algebras (Pitman, Boston, MA, 1983).Google Scholar
14.Elliott, G. A., Some C*-algebras with outer derivations, III, Annals Math. 106 (1977), 121–143.CrossRefGoogle Scholar
15.Fell, J. M. G., The dual spaces of C*-algebras, Trans. Am. Math. Soc. 94 (1960), 365–403.Google Scholar
16.Fell, J. M. G., The structure of algebras of operator fields, Acta Math. 106 (1961), 233–280.CrossRefGoogle Scholar
17.Frank, M. and Kirchberg, E., On conditional expectations of finite index, J. Operat. Theory 40 (1998), 87–111.Google Scholar
18.Gogić, I., Derivations which are inner as completely bounded maps, Operat. Matrices 4 (2010), 193–211.CrossRefGoogle Scholar
19.Gogić, I., Elementary operators and subhomogeneous C*-algebras, Proc. Edinb. Math. Soc. 54(1) (2011), 99–111.CrossRefGoogle Scholar
20.Gogić, I., Elementary operators and subhomogeneous C*-algebras, II, Banach J. Math. Analysis 5(1) (2011), 181–192.CrossRefGoogle Scholar
21.Gogić, I., Topologically finitely generated Hilbert C(X)-modules, Preprint (2011; available at http://web.math.hr/~ilja/preprints/TFGHM.pdf).Google Scholar
22.Kumar, A. and Sinclair, A. M., Equivalence of norms on operator space tensor products of C*-algebras, Trans. Am. Math. Soc. 350 (1998), 2033–2048.CrossRefGoogle Scholar
23.Lance, C., Hilbert C*-modules, London Mathematical Society Lecture Note Series, Volume 210 (Cambridge University Press, 1995).CrossRefGoogle Scholar
24.Magajna, B., Uniform approximation by elementary operators, Proc. Edinb. Math. Soc. 52 (3) (2009), 731–749.CrossRefGoogle Scholar
25.Murphy, G. J., C*-algebras and operator theory (Academic Press, San Diego, CA, 1990).Google Scholar
26.Pedersen, G. K., Approximating derivations on ideals of C*-algebras, Invent. Math. 45 (1978), 299–305.CrossRefGoogle Scholar
27.Phillips, N. C., Recursive subhomogeneous algebras, Trans. Am. Math. Soc. 359 (2007), 4595–4623.CrossRefGoogle Scholar
28.Raeburn, I. and Williams, D. P., Morita equivalence and continuous-trace C*-algebras, Mathematical Surveys and Monographs, Volume 60 (American Mathematical Society, Providence, RI, 1998).CrossRefGoogle Scholar
29.Somerset, D. W., The inner derivations and the primitive ideal space of a C*-algebra, J. Operat. Theory 29 (1993), 307–321.Google Scholar
30.Somerset, D. W., Inner derivations and primal ideals of C*-algebras, J. Lond. Math. Soc. (2) 50 (1994), 568–580.CrossRefGoogle Scholar
31.Somerset, D. W., The central Haagerup tensor product of a C*-algebra, J. Operat. Theory 39 (1998), 113–121.Google Scholar
32.Somerset, D. W., Derivations of 2-subhomogeneous C*-algebras, Proc. Edinb. Math. Soc. 43 (2000), 449–456.CrossRefGoogle Scholar
33.Takesaki, M., Theory of operator algebras, I (Springer, 1979).CrossRefGoogle Scholar
34.Wegge-Olsen, N. E., K-theory and C*-algebras (Oxford University Press, 1993).CrossRefGoogle Scholar
35.Williams, D. P., Crossed products C*-algebras, Mathematical Surveys and Monographs, Volume 134 (American Mathematical Society, Providence, RI, 2007).CrossRefGoogle Scholar