Article contents
BETWEEN THE PROBLEMS OF PÓLYA AND TURÁN
Published online by Cambridge University Press: 27 September 2012
Abstract
We investigate the behaviour of the function 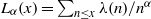 $L_{\alpha }(x) = \sum _{n\leq x}\lambda (n)/n^{\alpha }$, where
$L_{\alpha }(x) = \sum _{n\leq x}\lambda (n)/n^{\alpha }$, where 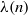 $\lambda (n)$ is the Liouville function and
$\lambda (n)$ is the Liouville function and  $\alpha $ is a real parameter. The case where
$\alpha $ is a real parameter. The case where 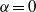 $\alpha =0$ was investigated by Pólya; the case
$\alpha =0$ was investigated by Pólya; the case 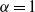 $\alpha =1$, by Turán. The question of the existence of sign changes in both of these cases is related to the Riemann hypothesis. Using both analytic and computational methods, we investigate similar problems for the more general family
$\alpha =1$, by Turán. The question of the existence of sign changes in both of these cases is related to the Riemann hypothesis. Using both analytic and computational methods, we investigate similar problems for the more general family 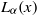 $L_{\alpha }(x)$, where
$L_{\alpha }(x)$, where 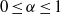 $0\leq \alpha \leq 1$, and their relationship to the Riemann hypothesis and other properties of the zeros of the Riemann zeta function. The case where
$0\leq \alpha \leq 1$, and their relationship to the Riemann hypothesis and other properties of the zeros of the Riemann zeta function. The case where 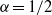 $\alpha =1/2$is of particular interest.
$\alpha =1/2$is of particular interest.
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 93 , Issue 1-2 , October 2012 , pp. 157 - 171
- Copyright
- Copyright © 2012 Australian Mathematical Publishing Association Inc.
Footnotes
Dedicated to the memory of Alf van der Poorten
References
- 4
- Cited by




