Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Schlanderer, Stefan C.
and
Sandberg, Richard D.
2013.
DNS of a Compliant Trailing-Edge Flow.
Goldstein, M. E.
Afsar, M. Z.
and
Leib, S. J.
2013.
Non-homogeneous rapid distortion theory on transversely sheared mean flows.
Journal of Fluid Mechanics,
Vol. 736,
Issue. ,
p.
532.
Jaworski, Justin
and
Peake, Nigel
2013.
Parametric guidance for turbulent noise reduction from poroelastic trailing edges and owls.
Cavalieri, André V.
Wolf, William R.
and
Jaworski, Justin
2014.
Acoustic scattering by finite poroelastic plates.
Clark, Ian
Devenport, William J.
Jaworski, Justin
Daly, Conor
Peake, Nigel
and
Glegg, Stewart A.
2014.
The Noise Generating and Suppressing Characteristics of Bio-Inspired Rough Surfaces.
Sarradj, Ennes
and
Geyer, Thomas
2014.
Symbolic regression modeling of noise generation at porous airfoils.
Journal of Sound and Vibration,
Vol. 333,
Issue. 14,
p.
3189.
Geyer, Thomas F.
and
Sarradj, Ennes
2014.
Trailing Edge Noise of Partially Porous Airfoils.
Cavalieri, André V.
Donadon, Maurício V.
and
Wolf, William
2015.
Acoustic scattering by finite composite plates.
Kisil, Anastasia V.
2015.
The relationship between a strip Wiener–Hopf problem and a line Riemann–Hilbert problem.
IMA Journal of Applied Mathematics,
Vol. 80,
Issue. 5,
p.
1569.
Gao, Jiali
Chu, Jinkui
Shang, Haixin
and
Guan, Le
2015.
Vibration attenuation performance of long-eared owl plumage.
Bioinspired, Biomimetic and Nanobiomaterials,
Vol. 4,
Issue. 3,
p.
187.
Hajian, Rozhin
and
Jaworski, Justin
2015.
The Steady Aerodynamics of Quiet Airfoils with Porosity Gradients.
孔, 德义
2015.
Study on Mechanism of Silent Flight of Owls.
Applied Physics,
Vol. 05,
Issue. 11,
p.
137.
Wolf, William
and
Cavalieri, André V.
2015.
A fast numerical framework for acoustic scattering by 3D poroelastic plates.
Mimani, Akhilesh
Moreau, Danielle
and
Doolan, Con J.
2015.
Experimental Application of Aeroacoustic Time-Reversal.
Kopania, Joanna M.
2015.
Bionics - Natural but Innovative Methods Improve the Aeroacoustic Engineering.
Applied Mechanics and Materials,
Vol. 806,
Issue. ,
p.
222.
Clark, Ian
Alexander, William N.
Devenport, William J.
Glegg, Stewart A.
Jaworski, Justin
Daly, Conor
and
Peake, Nigel
2015.
Bio-Inspired Trailing Edge Noise Control.
Weidenfeld, M.
and
Manela, A.
2016.
On the attenuating effect of permeability on the low frequency sound of an airfoil.
Journal of Sound and Vibration,
Vol. 375,
Issue. ,
p.
275.
Piantanida, Selene
Cavalieri, André V.
Wolf, William
Danadon, Mauricio
and
Jordan, Peter
2016.
Scattering of turbulent-jet wavepackets by a flexible composite plate.
Peake, Nigel
2016.
Fluid-Structure-Sound Interactions and Control.
p.
17.
Ayton, Lorna J.
2016.
The effects of poroelastic blade extensions on scattered noise.
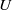 $U$. Special attention is paid to the limiting cases of porous-rigid and impermeable–elastic plate conditions. Asymptotic analysis of these special cases reveals parametric limits where the far-field acoustic power scales like
$U$. Special attention is paid to the limiting cases of porous-rigid and impermeable–elastic plate conditions. Asymptotic analysis of these special cases reveals parametric limits where the far-field acoustic power scales like 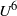 ${U}^{6} $ for a porous edge, and a new finite range of
${U}^{6} $ for a porous edge, and a new finite range of 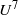 ${U}^{7} $ behaviour is found for an elastic edge, to be compared with the well-known
${U}^{7} $ behaviour is found for an elastic edge, to be compared with the well-known 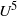 ${U}^{5} $ dependence for a rigid impermeable edge. Further numerical results attempt to address how trailing-edge noise may be mitigated by porosity and flexibility and seek to deepen the understanding of how owls hunt in acoustic stealth.
${U}^{5} $ dependence for a rigid impermeable edge. Further numerical results attempt to address how trailing-edge noise may be mitigated by porosity and flexibility and seek to deepen the understanding of how owls hunt in acoustic stealth.



