Hostname: page-component-8448b6f56d-wq2xx Total loading time: 0 Render date: 2024-04-18T12:27:02.869Z Has data issue: false hasContentIssue false
  • English
  • Français

Direct numerical simulation of a breaking inertia–gravity wave

Published online by Cambridge University Press:  28 March 2013

S. Remmler ,
M. D. Fruman  and
S. Hickel
S. Remmler
Affiliation:
Institute of Aerodynamics and Fluid Mechanics, Technische Universität München, D-85747 Garching bei München, Germany
M. D. Fruman
Affiliation:
Institute for Atmospheric and Environmental Sciences, Goethe-Universität Frankfurt, D-60438 Frankfurt am Main, Germany
S. Hickel*
Affiliation:
Institute of Aerodynamics and Fluid Mechanics, Technische Universität München, D-85747 Garching bei München, Germany
*
†Email address for correspondence: sh@tum.de
Get access Rights & Permissions [Opens in a new window]

Abstract

We have performed fully resolved three-dimensional numerical simulations of a statically unstable monochromatic inertia–gravity wave using the Boussinesq equations on an 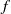$f$-plane with constant stratification. The chosen parameters represent a gravity wave with almost vertical direction of propagation and a wavelength of 3 km breaking in the middle atmosphere. We initialized the simulation with a statically unstable gravity wave perturbed by its leading transverse normal mode and the leading instability modes of the time-dependent wave breaking in a two-dimensional space. The wave was simulated for approximately 16 h, which is twice the wave period. After the first breaking triggered by the imposed perturbation, two secondary breaking events are observed. Similarities and differences between the three-dimensional and previous two-dimensional solutions of the problem and effects of domain size and initial perturbations are discussed.

JFM classification

Geophysical and Geological Flows: Atmospheric flows Geophysical and Geological Flows: Internal waves Geophysical and Geological Flows: Stratified flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 722 , 10 May 2013 , pp. 424 - 436
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Achatz, U. 2005 On the role of optimal perturbations in the instability of monochromatic gravity waves. Phys. Fluids 17 (9), 094107.Google Scholar
Achatz, U. 2007 The primary nonlinear dynamics of modal and nonmodal perturbations of monochromatic inertia gravity waves. J. Atmos. Sci. 64, 74–95.Google Scholar
Achatz, U. & Schmitz, G. 2006a Optimal growth in inertia-gravity wave packets: energetics, long-term development, and three-dimensional structure. J. Atmos. Sci. 63, 414–434.Google Scholar
Achatz, U. & Schmitz, G. 2006b Shear and static instability of inertia-gravity wave packets: short-term modal and nonmodal growth. J. Atmos. Sci. 63, 397–413.CrossRefGoogle Scholar
Afanasyev, Y. D. & Peltier, W. R. 2001 Numerical simulations of internal gravity wave breaking in the middle atmosphere: the influence of dispersion and three-dimensionalization. J. Atmos. Sci. 58, 132–153.Google Scholar
Andreassen, Ø., Øyvind Hvidsten, P., Fritts, D. C. & Arendt, S. 1998 Vorticity dynamics in a breaking internal gravity wave. Part 1. Initial instability evolution. J. Fluid Mech. 367, 27–46.Google Scholar
Andreassen, Ø, Wasberg, C. E., Fritts, D. C. & Isler, J. R. 1994 Gravity wave breaking in two and three dimensions 1. Model description and comparison of two-dimensional evolutions. J. Geophys. Res. 99, 8095–8108.Google Scholar
Blumen, W. & McGregor, C. D. 1976 Wave drag by three-dimensional mountain lee-waves in nonplanar shear flow. Tellus 28 (4), 287–298.Google Scholar
Bretherton, F. P. 1969 Waves and turbulence in stably stratified fluids. Radio Sci. 4 (12), 1279–1287.Google Scholar
Chun, H.-Y. & Baik, J.-J. 1998 Momentum flux by thermally induced internal gravity waves and its approximation for large-scale models. J. Atmos. Sci. 55, 3299–3310.Google Scholar
Dörnbrack, A. 1998 Turbulent mixing by breaking gravity waves. J. Fluid Mech. 375, 113–141.Google Scholar
Drazin, P. G. 1977 On the instability of an internal gravity wave. Proc. R. Soc. Lond. A 356 (1686), 411–432.Google Scholar
Dunkerton, T. J. 1997a The role of gravity waves in the quasi-biennial oscillation. J. Geophys. Res. 102, 26053–26076.Google Scholar
Dunkerton, T. J. 1997b Shear instability of internal inertia-gravity waves. J. Atmos. Sci. 54, 1628–1641.2.0.CO;2>CrossRefGoogle Scholar
Fritts, D. C. & Alexander, M. J. 2003 Gravity wave dynamics and effects in the middle atmosphere. Rev. Geophys. 41, 1003.Google Scholar
Fritts, D. C., Isler, J. R. & Andreassen, Ø. 1994 Gravity wave breaking in two and three dimensions 2. Three-dimensional evolution and instability structure. J. Geophys. Res. 99, 8109–8124.Google Scholar
Fritts, D. C., Wang, L., Werne, J., Lund, T. & Wan, K. 2009 Gravity wave instability dynamics at high Reynolds numbers. Parts I and II. J. Atmos. Sci. 66 (5), 1126–1171.Google Scholar
Fruman, M. D. & Achatz, U. 2012 Secondary instabilities in breaking inertia-gravity waves. J. Atmos. Sci. 69, 303–322.Google Scholar
Holton, J. R. 1982 The role of gravity wave induced drag and diffusion in the momentum budget of the mesosphere. J. Atmos. Sci. 39, 791–799.Google Scholar
Houghton, J. T. 1978 The stratosphere and mesosphere. Q. J. R. Meteorol. Soc. 104 (439), 1–29.Google Scholar
Klostermeyer, J. 1982 On parametric instabilities of finite-amplitude internal gravity waves. J. Fluid Mech. 119, 367–377.Google Scholar
Lelong, M.-P. & Dunkerton, T. J. 1998 Inertia-gravity wave breaking in three dimensions. Parts I and II. J. Atmos. Sci. 55, 2473–2501.Google Scholar
Lilly, D. K. 1972 Wave momentum flux – A GARP problem. Bull. Am. Meteorol. Soc. 53, 17–23.Google Scholar
Lindzen, R. S. 1981 Turbulence and stress owing to gravity wave and tidal breakdown. J. Geophys. Res. 86, 9707–9714.Google Scholar
McLandress, C. 1998 On the importance of gravity waves in the middle atmosphere and their parameterization in general circulation models. J. Atmos. Sol.-Terr. Phys. 60 (14), 1357–1383.Google Scholar
Mied, R. P. 1976 The occurrence of parametric instabilities in finite-amplitude internal gravity waves. J. Fluid Mech. 78 (4), 763–784.Google Scholar
Nappo, C. J. 2002 An Introduction to Atmospheric Gravity Waves. Academic.Google Scholar
Remmler, S. & Hickel, S. 2012a Direct and large eddy simulation of stratified turbulence. Intl J. Heat Fluid Flow 35, 13–24.Google Scholar
Remmler, S. & Hickel, S. 2012b Spectral structure of stratified turbulence: direct numerical simulations and predictions by large eddy simulation. Theor. Comput. Fluid Dyn. Published online: doi:10.1007/s00162-012-0259-9.Google Scholar
Sawyer, J. S. 1959 The introduction of the effects of topography into methods of numerical forecasting. Q. J. R. Meteorol. Soc. 85 (363), 31–43.Google Scholar
Shu, C.-W. 1988 Total-variation-diminishing time discretizations. SIAM J. Sci. Stat. Comput. 9 (6), 1073–1084.Google Scholar
Thorpe, S. A. 1977 Turbulence and mixing in a scottish loch. Phil. Trans. R. Soc. Lond. A 286 (1334), 125–181.Google Scholar
Winters, K. B. & D’Asaro, E. A. 1994 Three-dimensional wave instability near a critical level. J. Fluid Mech. 272, 255–284.CrossRefGoogle Scholar
Yamazaki, Y., Ishihara, T. & Kaneda, Y. 2002 Effects of wavenumber truncation on high-resolution direct numerical simulation of turbulence. J. Phys. Soc. Japan 71, 777–781.Google Scholar