Hostname: page-component-8448b6f56d-m8qmq Total loading time: 0 Render date: 2024-04-20T09:18:17.425Z Has data issue: false hasContentIssue false
  • English
  • Français

The tangent complex and Hochschild cohomology of 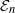$\mathcal {E}_n$-rings

Part of: Local theory Homological algebra Homology and cohomology theories

Published online by Cambridge University Press:  10 December 2012

John Francis
John Francis*
Affiliation:
Department of Mathematics, Northwestern University, Evanston, IL 60208-2370, USA (email: jnkf@northwestern.edu)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this work, we study the deformation theory of 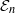${\mathcal {E}}_n$-rings and the 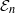${\mathcal {E}}_n$ analogue of the tangent complex, or topological André–Quillen cohomology. We prove a generalization of a conjecture of Kontsevich, that there is a fiber sequence $A[n-1] \rightarrow T_A\rightarrow {\mathrm {HH}}^*_{{\mathcal {E}}_{n}}\!(A)[n]$, relating the 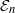${\mathcal {E}}_n$-tangent complex and 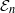${\mathcal {E}}_n$-Hochschild cohomology of an 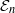${\mathcal {E}}_n$-ring 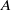$A$. We give two proofs: the first is direct, reducing the problem to certain stable splittings of configuration spaces of punctured Euclidean spaces; the second is more conceptual, where we identify the sequence as the Lie algebras of a fiber sequence of derived algebraic groups, 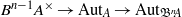$B^{n-1}A^\times \rightarrow {\mathrm {Aut}}_A\rightarrow {\mathrm {Aut}}_{{\mathfrak B}^n\!A}$. Here 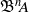${\mathfrak B}^n\!A$ is an enriched 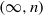$(\infty ,n)$-category constructed from 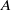$A$, and ${\mathcal {E}}_n$-Hochschild cohomology is realized as the infinitesimal automorphisms of 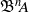${\mathfrak B}^n\!A$. These groups are associated to moduli problems in ${\mathcal {E}}_{n+1}$-geometry, a less commutative form of derived algebraic geometry, in the sense of the work of Toën and Vezzosi and the work of Lurie. Applying techniques of Koszul duality, this sequence consequently attains a nonunital 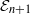${\mathcal {E}}_{n+1}$-algebra structure; in particular, the shifted tangent complex 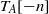$T_A[-n]$ is a nonunital 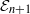${\mathcal {E}}_{n+1}$-algebra. The ${\mathcal {E}}_{n+1}$-algebra structure of this sequence extends the previously known 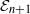${\mathcal {E}}_{n+1}$-algebra structure on 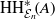${\mathrm {HH}}^*_{{\mathcal {E}}_{n}}\!(A)$, given in the higher Deligne conjecture. In order to establish this moduli-theoretic interpretation, we make extensive use of factorization homology, a homology theory for framed $n$-manifolds with coefficients given by ${\mathcal {E}}_n$-algebras, constructed as a topological analogue of Beilinson and Drinfeld’s chiral homology. We give a separate exposition of this theory, developing the necessary results used in our proofs.

Keywords

-algebrasdeformation theorythe tangent complexHochschild cohomologyfactorization homologytopological chiral homologyKoszul dualityoperads-categories

MSC classification

Secondary: 14B12: Local deformation theory, Artin approximation, etc. 55N35: Other homology theories 18G55: Homotopical algebra
Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 3 , March 2013 , pp. 430 - 480
Copyright
Copyright © 2012 The Author(s)

References

[And10]Andrade, R., From manifolds to invariants of E n-algebras, PhD thesis, Massachusetts Institute of Technology (2010).Google Scholar
[Ang11]Angeltveit, V., Uniqueness of Morava K-theory, Compositio Math. 147 (2011), 633–648.CrossRefGoogle Scholar
[AFT12]Ayala, D., Francis, J. and Tanaka, H., Structured singular manifolds and factorization homology, Preprint (2012), arXiv:1206.5164.Google Scholar
[Bas99]Basterra, M., André–Quillen cohomology of commutative S-algebras, J. Pure Appl. Algebra 144 (1999), 111–143.CrossRefGoogle Scholar
[BM05]Basterra, M. and Mandell, M., Homology and cohomology of $E_\infty $ ring spectra, Math. Z. 249 (2005), 903–944.CrossRefGoogle Scholar
[BM10]Basterra, M. and Mandell, M., The multiplication on $BP$, Preprint (2010), arXiv:1101.0023.Google Scholar
[BD04]Beilinson, A. and Drinfeld, V., Chiral algebras, American Mathematical Society Colloquium Publications, vol. 51 (American Mathematical Society, Providence, RI, 2004).CrossRefGoogle Scholar
[BFN10]Ben-Zvi, D., Francis, J. and Nadler, D., Integral transforms and Drinfeld centers in derived algebraic geometry, J. Amer. Math. Soc. 23 (2010), 909–966.CrossRefGoogle Scholar
[BV73]Boardman, J. M. and Vogt, R., Homotopy invariant algebraic structures on topological spaces, Lecture Notes in Mathematics, vol. 347 (Springer, Berlin, 1973).CrossRefGoogle Scholar
[Chi05]Ching, M., Bar constructions for topological operads and the Goodwillie derivatives of the identity, Geom. Topol. 9 (2005), 833–933.CrossRefGoogle Scholar
[Coh76]Cohen, F., The homology of 𝒞n+1-spaces, n≥0, Lecture Notes in Mathematics, vol. 533 (Springer, Berlin, 1976), 207–351.Google Scholar
[CG]Costello, K. and Gwilliam, O., Factorization algebras in perturbative quantum field theory, Preprint, http://www.math.northwestern.edu/∼costello/renormalization.Google Scholar
[Dun88]Dunn, Gerald., Tensor product of operads and iterated loop spaces, J. Pure Appl. Algebra 50 (1988), 237–258.CrossRefGoogle Scholar
[Fra08]Francis, J., Derived algebraic geometry over ℰn-rings, PhD thesis, Massachusetts Institute of Technology (2008).Google Scholar
[Fra12]Francis, J., Factorization homology of topological manifolds, Preprint (2012), arXiv:1206.5522.Google Scholar
[FG11]Francis, J. and Gaitsgory, D., Chiral Koszul duality, Preprint (2011), arXiv:1103.5803v1.CrossRefGoogle Scholar
[Fre00]Fresse, B., On the homotopy of simplicial algebras over an operad, Trans. Amer. Math. Soc. 352 (2000), 4113–4141.CrossRefGoogle Scholar
[Fre11]Fresse, B., Koszul duality of $E_n$-operads, Selecta Math. (N.S.) 17 (2011), 363–434.CrossRefGoogle Scholar
[Gep]Gepner, D., Enriched $\infty $-categories, in preparation.Google Scholar
[GJ94]Getzler, E. and Jones, J., Operads, homotopy algebra and iterated integrals for double loop spaces, Preprint (1994), arXiv:hep-th/9403055.Google Scholar
[GTZ]Ginot, G., Tradler, T. and Zeinalian, M., Derived higher Hochschild homology, topological chiral homology and factorization algebras, Preprint.Google Scholar
[GK94]Ginzburg, V. and Kapranov, M., Koszul duality for operads, Duke Math. J. 76 (1994), 203–272.CrossRefGoogle Scholar
[GH00]Goerss, P. and Hopkins, M., Andé-Quillen (co)-homology for simpli- cial algebras over simplicial operads, in Une dégustation topologique: homotopy theory in the Swiss Alps (Arolla, 1999), Contemporary Mathematics, vol. 265 (American Mathematical Society, Providence, RI, 2000), 41–85.CrossRefGoogle Scholar
[Goo03]Goodwillie, T., Calculus III: Taylor Series, Geom. Topol. 7 (2003), 645–711.CrossRefGoogle Scholar
[Hu06]Hu, Po., Higher string topology on general spaces, Proc. Lond. Math. Soc. (3) 93 (2006), 515–544.CrossRefGoogle Scholar
[HKV06]Hu, P., Kriz, I. and Voronov, A., On Kontsevich’s Hochschild cohomology conjecture, Compositio Math. 142 (2006), 143–168.CrossRefGoogle Scholar
[Joy02]Joyal, A., Quasi-categories and Kan complexes, J. Pure Appl. Algebra 175 (2002), 207–222.CrossRefGoogle Scholar
[Kel04]Keller, B., Hochschild cohomology and derived Picard groups, J. Pure Appl. Algebra 190 (2004), 177–196.CrossRefGoogle Scholar
[Kis64]Kister, J., Microbundles are fibre bundles, Ann. of Math. (2) 80 (1964), 190–199.CrossRefGoogle Scholar
[Kon99]Kontsevich, M., Operads and motives in deformation quantization, Lett. Math. Phys. 48 (1999), 35–72.CrossRefGoogle Scholar
[KS]Kontsevich, M. and Soibelman, , Deformation theory, Vol. 1, unpublished book draft, www.math.ksu.edu/∼soibel/Book-vol1.ps.Google Scholar
[LV]Lambrechts, P. and Volić, I., Formality of the little $N$-discs operad, Preprint.Google Scholar
[Laz01]Lazarev, A., Homotopy theory of A ∞ ring spectra and applications to $M{\rm U}$-modules, K-Theory 24 (2001), 243–281.CrossRefGoogle Scholar
[Lur]Lurie, J., Moduli problems for ring spectra, Preprint, http://www.math.harvard.edu/∼lurie.Google Scholar
[Lur06]Lurie, J., Derived algebraic geometry 1: stable $\infty $-categories, Preprint, arXiv:math.CT/0608228.Google Scholar
[Lur07a]Lurie, J., Derived algebraic geometry 2: noncommutative algebra, Preprint (2007), arXiv:math.CT/0702299.Google Scholar
[Lur07b]Lurie, J., Derived algebraic geometry 3: commutative algebra, Preprint (2007), arXiv:math.CT/0703204.Google Scholar
[Lur07c]Lurie, J., Derived algebraic geometry 4: deformation theory, Preprint (2007), arXiv:math.CT/0709.3091v2.Google Scholar
[Lur09a]Lurie, J., Derived algebraic geometry 5: structured spaces, Preprint (2009), arXiv:math.CT/0905.0459v1.Google Scholar
[Lur09b]Lurie, J., Derived algebraic geometry 6: $E_k$-algebras, Preprint, arXiv:math.CT/0911.0018.Google Scholar
[Lur09c]Lurie, J., Higher topos theory, Annals of Mathematics Studies, vol. 170 (Princeton University Press, Princeton, NJ, 2009).CrossRefGoogle Scholar
[May72]May, J. P., The geometry of iterated loop spaces, Lectures Notes in Mathematics, vol. 271 (Springer, Berlin, 1972).CrossRefGoogle Scholar
[MS02]McClure, J. and Smith, J., A solution of Deligne’s Hochschild cohomology conjecture, in Recent progress in homotopy theory, Contemporary Mathematics, vol. 293 (American Mathematical Society, Providence, RI, 2002), 153–194.CrossRefGoogle Scholar
[McD75]McDuff, D., Configuration spaces of positive and negative particles, Topology 14 (1975), 91–107.CrossRefGoogle Scholar
[MW10]Morrison, S. and Walker, K., Blob complex, Preprint (2010), arXiv:1009.5025v3.Google Scholar
[Qui70]Quillen, D., On the (co-) homology of commutative rings, in Applications of Categorical Algebra, Proceedings of Symposia in Pure Mathematics, vol. 17 (American Mathematical Society, Providence, RI, 1970), 65–87.CrossRefGoogle Scholar
[Rez96]Rezk, C., Spaces of algebra structures and cohomology of operads, PhD thesis, Massachusetts Institute of Technology (1996).Google Scholar
[Sal01]Salvatore, P., Configuration spaces with summable labels, in Cohomological methods in homotopy theory (Bellaterra, 1998), Progress in Mathematics, vol. 196 (Birkhäuser, Basel, 2001), 375–395.CrossRefGoogle Scholar
[SW03]Salvatore, P. and Wahl, N., Framed discs operads and Batalin-Vilkovisky algebras, Q. J. Math. 54 (2003), 213–231.CrossRefGoogle Scholar
[Sch68]Schlessinger, M., Functors of Artin rings, Trans. Amer. Math. Soc. 130 (1968), 208–222.CrossRefGoogle Scholar
[SS85]Schlessinger, M. and Stasheff, J., The Lie algebra structure of tangent cohomology and deformation theory, J. Pure and Appl. Algebra 38 (1985), 313–322.CrossRefGoogle Scholar
[Tam00]Tamarkin, D., The deformation complex of a $d$-algebra is a $(d+1)$-algebra, Preprint (2000), arXiv:math/0010072v1.Google Scholar
[Tho10]Thomas, J., Kontsevich’s swiss cheese conjecture, PhD thesis, Northwestern University (2010).Google Scholar
[Toe09]Toën, B., Higher and derived stacks: a global overview, in Algebraic geometry – Seattle 2005. Part 1, Proceedings of Symposia in Pure Mathematics, vol. 80 (American Mathematical Society, Providence, RI, 2009), 435–487.Google Scholar
[BG05]Toën, B. and Vezzosi, G., Homotopical algebraic geometry I: topos theory, Adv. Math. 193 (2005), 257–372.CrossRefGoogle Scholar
[BG08]Toën, B. and Vezzosi, G., Homotopical algebraic geometry. II. Geometric stacks and applications, Mem. Amer. Math. Soc. 193 (2008).Google Scholar