Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Persson, Tomas
and
Reeve, Henry W. J.
2015.
A Frostman-Type Lemma for Sets with Large Intersections, and an Application to Diophantine Approximation.
Proceedings of the Edinburgh Mathematical Society,
Vol. 58,
Issue. 2,
p.
521.
BAKER, SIMON
2018.
Approximation properties of -expansions II.
Ergodic Theory and Dynamical Systems,
Vol. 38,
Issue. 5,
p.
1627.
Baker, Simon
2023.
Overlapping Iterated Function Systems from the Perspective of Metric Number Theory.
Memoirs of the American Mathematical Society,
Vol. 287,
Issue. 1428,
Baker, Simon
2024.
Intrinsic Diophantine approximation for overlapping iterated function systems.
Mathematische Annalen,
Vol. 388,
Issue. 3,
p.
3259.




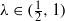 and
and 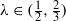 , the upper bound of
, the upper bound of 