Hostname: page-component-8448b6f56d-c4f8m Total loading time: 0 Render date: 2024-04-20T12:35:05.076Z Has data issue: false hasContentIssue false
  • English
  • Français

Complexity for modules over the classical Lie superalgebra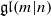

Part of: Lie algebras and Lie superalgebras General commutative ring theory

Published online by Cambridge University Press:  25 July 2012

Brian D. Boe ,
Jonathan R. Kujawa  and
Daniel K. Nakano
Brian D. Boe
Affiliation:
Department of Mathematics, University of Georgia, Athens, GA 30602, USA (email: brian@math.uga.edu)
Jonathan R. Kujawa
Affiliation:
Department of Mathematics, University of Oklahoma, Norman, OK 73019, USA (email: kujawa@math.ou.edu)
Daniel K. Nakano
Affiliation:
Department of Mathematics, University of Georgia, Athens, GA 30602, USA (email: nakano@math.uga.edu)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 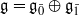be a classical Lie superalgebra and let ℱ be the category of finite-dimensional 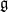-supermodules which are completely reducible over the reductive Lie algebra 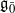. In [B. D. Boe, J. R. Kujawa and D. K. Nakano, Complexity and module varieties for classical Lie superalgebras, Int. Math. Res. Not. IMRN (2011), 696–724], we demonstrated that for any module M in ℱ the rate of growth of the minimal projective resolution (i.e. the complexity of M) is bounded by the dimension of 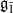. In this paper we compute the complexity of the simple modules and the Kac modules for the Lie superalgebra 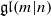. In both cases we show that the complexity is related to the atypicality of the block containing the module.

Keywords

Lie superalgebrasrepresentation theorycohomologysupport varietiescomplexity

MSC classification

Secondary: 17B56: Cohomology of Lie (super)algebras 17B10: Representations, algebraic theory (weights) 13A50: Actions of groups on commutative rings; invariant theory
Type
Research Article
Information
Compositio Mathematica , Volume 148 , Issue 5 , September 2012 , pp. 1561 - 1592
Copyright
Copyright © Foundation Compositio Mathematica 2012

References

[Alp77]Alperin, J. L., Periodicity in groups, Illinois J. Math. 21 (1977), 776–783.Google Scholar
[BR07]Beck, M. and Robins, S., Computing the continuous discretely: integer-point enumeration in polyhedra, Undergraduate Texts in Mathematics (Springer, New York, 2007).Google Scholar
[BKN09]Boe, B. D., Kujawa, J. R. and Nakano, D. K., Cohomology and support varieties for Lie superalgebras II, Proc. Lond. Math. Soc. 98 (2009), 19–44.Google Scholar
[BKN10]Boe, B. D., Kujawa, J. R. and Nakano, D. K., Cohomology and support varieties for Lie superalgebras, Trans. Amer. Math. Soc. 362 (2010), 6551–6590.Google Scholar
[BKN11]Boe, B. D., Kujawa, J. R. and Nakano, D. K., Complexity and module varieties for classical Lie superalgebras, Int. Math. Res. Not. IMRN (3) (2011), 696–724.Google Scholar
[BW80]Borel, A. and Wallach, N. R., Continuous cohomology, discrete subgroups, and representations of reductive groups, Annals of Mathematics Studies, vol. 94 (Princeton University Press, Princeton, NJ, 1980).Google Scholar
[Bru03]Brundan, J., Kazhdan-Lusztig polynomials and character formulae for the Lie superalgebra 𝔤𝔩(m|n), J. Amer. Math. Soc. 16 (2003), 185–231 (electronic).CrossRefGoogle Scholar
[BS12]Brundan, J. and Stroppel, C., Highest weight categories arising from Khovanov’s diagram algebra IV: the general linear supergroup, J. Eur. Math. Soc. 14 (2012), 373–419.Google Scholar
[CPS88]Cline, E. T., Parshall, B. J. and Scott, L. L., Finite-dimensional algebras and highest weight categories, J. Reine Angew. Math. 391 (1988), 85–99.Google Scholar
[DNP12]Drupieski, C. M., Nakano, D. K. and Parshall, B. J., Differentiating the Weyl generic dimension formula with applications to support varieties, Adv. Math. 229 (2012), 2656–2668.Google Scholar
[DS05]Duflo, M. and Serganova, V., On associated variety for Lie superalgebras, Preprint (2005), arXiv:math/0507198.Google Scholar
[FS97]Friedlander, E. M. and Suslin, A., Cohomology of finite group schemes over a field, Invent. Math. 127 (1997), 209–270.Google Scholar
[GKP11]Geer, N., Kujawa, J. and Patureau-Mirand, B., Generalized trace and modified dimension functions on ribbon categories, Selecta Math. 17 (2011), 453–504.Google Scholar
[GW98]Goodman, R. and Wallach, N. R., Representations and invariants of the classical groups, Encyclopedia of Mathematics and its Applications, vol. 68 (Cambridge University Press, Cambridge, 1998).Google Scholar
[GS10]Gruson, C. and Serganova, V., Cohomology of generalized supergrassmannians and character formulae for basic classical Lie superalgebras, Proc. Lond. Math. Soc. (3) 101 (2010), 852–892.Google Scholar
[Har92]Harris, J., Algebraic geometry: a first course, Graduate Texts in Mathematics, vol. 133 (Springer, New York, 1992).CrossRefGoogle Scholar
[HN02]Hemmer, D. J. and Nakano, D. K., Support varieties for modules over symmetric groups, J. Algebra 254 (2002), 422–440.CrossRefGoogle Scholar
[Jan03]Jantzen, J. C., Representations of algebraic groups, Mathematical Surveys and Monographs, vol. 107, second edition (American Mathematical Society, Providence, RI, 2003).Google Scholar
[Kac77]Kac, V. G., Lie superalgebras, Adv. Math. 26 (1977), 8–96.CrossRefGoogle Scholar
[Kac78]Kac, V. G., Representations of classical Lie superalgebras, in Differential geometrical methods in mathematical physics II (Proceedings, University of Bonn, July 13–16, 1977), Lecture Notes in Mathematics, vol. 676 (Springer, Berlin, 1978), 597–626.Google Scholar
[KW94]Kac, V. G. and Wakimoto, M., Integrable highest weight modules over affine superalgebras and number theory, in Lie theory and geometry, Progress in Mathematics, vol. 123 (Birkhäuser, Boston, MA, 1994), 415–456.CrossRefGoogle Scholar
[LNZ10]Lehrer, G. I., Nakano, D. K. and Zhang, R. B., Detecting cohomology for Lie superalgebras, Adv. Math. 228 (2011), 2098–2115.Google Scholar
[NPV02]Nakano, D. K., Parshall, B. J. and Vella, D. C., Support varieties for algebraic groups, J. Reine Angew. Math. 547 (2002), 15–49.Google Scholar
[Nat00]Nathanson, M. B., Elementary methods in number theory, Graduate Texts in Mathematics, vol. 195 (Springer, New York, 2000).Google Scholar
[Sch69]Schmid, W., Die Randwerte holomorpher Funktionen auf hermitesch symmetrischen Räumen, Invent. Math. 9 (1969/1970), 61–80.CrossRefGoogle Scholar
[Ser10]Serganova, V., On the superdimension of an irreducible representation of a basic classical Lie superalgebra, in Supersymmetry in Mathematics and Physics (UCLA, Los Angeles, USA 2010), Lecture Notes in Mathematics, vol. 2027 eds Ferrara, S., Fioresi, R. and Varadarajan, V. S. (Springer, Berlin, 2011), 253–273.Google Scholar
[Ser96]Serganova, V., Kazhdan-Lusztig polynomials and character formula for the Lie superalgebra , Selecta Math. (N.S.) 2 (1996), 607–651.Google Scholar
[SZ07]Su, Y. and Zhang, R. B., Character and dimension formulae for general linear superalgebra, Adv. Math. 211 (2007), 1–33.Google Scholar
[UGA07] University of Georgia VIGRE Algebra Group, Support varieties for Weyl modules over bad primes, J. Algebra 312 (2007), 602–633.CrossRefGoogle Scholar