Hostname: page-component-8448b6f56d-dnltx Total loading time: 0 Render date: 2024-04-24T05:51:52.126Z Has data issue: false hasContentIssue false
  • English
  • Français

Magnetohydrodynamic drift equations: from Langmuir circulations to magnetohydrodynamic dynamo?

Published online by Cambridge University Press:  23 March 2012

V. A. Vladimirov
V. A. Vladimirov*
Affiliation:
Department of Mathematics, University of York, Heslington, York YO10 5DD, UK
*
†Email address for correspondence: vv500@york.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We derive the closed system of averaged magnetohydrodynamic (MHD) equations for general oscillating flows. The used small parameter of our asymptotic theory is the dimensionless inverse frequency, and the leading term for a velocity field is chosen to be purely oscillating. The employed mathematical approach combines the two-timing method and the notion of a distinguished limit. The properties of commutators are used to simplify calculations. The derived averaged equations are similar to the original MHD equations, but surprisingly (instead of the commonly expected Reynolds stresses) a drift velocity plays a part of an additional advection velocity. In the special case of a vanishing magnetic field 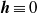, the averaged equations produce the Craik–Leibovich equations for Langmuir circulations (which can be called ‘vortex dynamo’). We suggest that, since the mathematical structure of the full averaged equations for 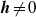is similar to those for 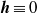, these full equations could lead to a possible mechanism of MHD dynamo, such as the generation of the magnetic field of the Earth.

JFM classification

MHD and Electrohydrodynamics: Dynamo theory Mathematical Foundations: General fluid mechanics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 698 , 10 May 2012 , pp. 51 - 61
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Andrews, D. & McIntyre, M. E. 1978 An exact theory of nonlinear waves on a Lagrangian-mean flow. J. Fluid Mech. 89, 609–646.CrossRefGoogle Scholar
2. Batchelor, G. K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
3. Childress, s. & Gilbert, A. D. 1995 Stretch, Twist, Fold: The Fast Dynamo. Springer.Google Scholar
4. Craik, A. D. D. 1982 The drift velocity of water waves. J. Fluid Mech. 116, 187–205.Google Scholar
5. Craik, A. D. D. 1985 Wave Interactions and Fluid Flows. Cambridge University Press.Google Scholar
6. Craik, A. D. D. & Leibovich, S. 1976 A rational model for Langmuir circulations. J. Fluid Mech. 73 (3), 401–426.CrossRefGoogle Scholar
7. Debnath, L. 1994 Nonlinear Water Waves. Academic Press.Google Scholar
8. Frisch, U. 1985 Turbulence. The Legacy of A. N. Kolmogorov. Cambridge University Press.Google Scholar
9. Herreman, W. & Lesaffre, P. 2011 Stokes drift dynamos. J. Fluid Mech. 679 (3), 32–57.CrossRefGoogle Scholar
10. Hughes, D. W. & Proctor, M. R. E. 2010 Turbulent magnetic diffusivity tensor for time-dependent mean fields. Phys. Rev. Lett. 104, 024503.CrossRefGoogle ScholarPubMed
11. Ilin, K. I. & Morgulis, A. B. 2011 Steady streaming between two vibrating planes at high Reynolds numbers. Phys. Fluid Dyn., arXiv:1108.2710v1.Google Scholar
12. Kevorkian, J. & Cole, J. D. 1996 Multiple Scale and Singular Perturbation Method, Applied Mathematical Sciences, vol. 114 , Springer.Google Scholar
13. Lamb, H. 1932 Hydrodynamics, 6th edn. Cambridge University Press.Google Scholar
14. Leibovich, S. 1983 The forms and dynamics of Langmuir circulations. Annu. Rev. Fluid Mech. 15, 391–427.Google Scholar
15. Longuet-Higgins, M. S. 1953 Mass transport in water waves. Phil. Trans. R. Soc. Lond. A 245, 535–581.Google Scholar
16. Moffatt, H. K. 1978 Magnetic Field Generation in Electrically Conducting Fluid. Cambridge University Press.Google Scholar
17. Moffatt, H. K. 1983 Transport effects associated with turbulence with particular attention to the influence of helicity. Rep. Prog. Phys. 46, 621–664.Google Scholar
18. Nayfeh, A. H. 1973 Perturbation Methods. John Wiley & Sons.Google Scholar
19. Riley, N. 2001 Steady streaming. Annu. Rev. Fluid Mech. 33, 43–65.Google Scholar
20. Roberts, P. H. & Soward, A. M. 1992 Dynamo theory. Annu. Rev. Fluid Mech. 24, 459–512.Google Scholar
21. Soward, A. M. & Roberts, P. H. 2010 The hybrid Euler–Lagrange procedure using an extension of Moffatt’s method. J. Fluid Mech. 661, 45–72.Google Scholar
22. Stokes, G. G. 1847 On the theory of oscillatory waves. Trans. Camb. Phil. Soc. 8, 441–455 (reprinted in Mathematical and Physical Papers, vol. 1, pp. 197–219).Google Scholar
23. Thorpe, S. A. 2004 Langmuir circulation. Annu. Rev. Fluid Mech. 36, 55–79.Google Scholar
24. Vladimirov, V. A. 1985a An example of equivalence between density stratification and rotation. Sov. Phys. Dokl. 30 (9), 748–750 (translated from Russian).Google Scholar
25. Vladimirov, V. A. 1985b Analogy between the effects of density stratification and rotation. J. Appl. Mech. Tech. Phys. 26 (3), 353–362 (translated from Russian).Google Scholar
26. Vladimirov, V. A. 2005 Vibrodynamics of pendulum and submerged solid. J. Math. Fluid Mech. 7, S397–S412.CrossRefGoogle Scholar
27. Vladimirov, V. A. 2008 Viscous flows in a half-space caused by tangential vibrations on its boundary. Stud. Appl. Maths 121 (4), 337–367.CrossRefGoogle Scholar
28. Vladimirov, V. A. 2010 Admixture and drift in oscillating fluid flows. Phys. Fluid Dyn., arXiv:1009.4085v1.Google Scholar
29. Vladimirov, V. A. 2011 Theory of non-degenerate oscillatory flows. Phys. Fluid Dyn., arXiv:1110.3633v2.Google Scholar
30. Vladimirov, V. A., Moffatt, H. K. & Ilin, K. I. 1996 On general transformations and variational principles for the magnetohydrodynamics of ideal fluids. Part 2. Stability criteria for two-dimensional flows. J. Fluid Mech. 329, 187–207.Google Scholar
31. Yudovich, V. I. 2006 Vibrodynamics and vibrogeometry of mechanical systems with constraints (in Russian). Usp. Mekh. 4 (3), 26–158.Google Scholar
32. Zheligovsky, V. A. 2009 Mathematical Stability Theory for MHD Flows with Respect to Long-Wave Perturbations. Krasand (in Russian).Google Scholar