Article contents
1-loop graphs and configuration space integral for embedding spaces
Published online by Cambridge University Press: 10 January 2012
Abstract
We will construct differential forms on the embedding spaces Emb(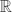 j,
j, 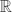 n) for n − j ≥ 2 using configuration space integral associated with 1-loop graphs, and show that some linear combinations of these forms are closed in some dimensions. There are other dimensions in which we can show the closedness if we replace Emb(
n) for n − j ≥ 2 using configuration space integral associated with 1-loop graphs, and show that some linear combinations of these forms are closed in some dimensions. There are other dimensions in which we can show the closedness if we replace Emb(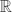 j,
j, 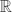 n) by Emb(
n) by Emb(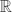 j,
j, 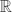 n), the homotopy fiber of the inclusion Emb(
n), the homotopy fiber of the inclusion Emb(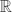 j,
j, 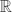 n) ↪ Imm(
n) ↪ Imm(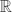 j,
j, 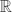 n). We also show that the closed forms obtained give rise to nontrivial cohomology classes, evaluating them on some cycles of Emb(
n). We also show that the closed forms obtained give rise to nontrivial cohomology classes, evaluating them on some cycles of Emb(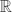 j,
j, 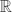 n) and Emb(
n) and Emb(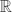 j,
j, 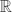 n). In particular we obtain nontrivial cohomology classes (for example, in H3(Emb(
n). In particular we obtain nontrivial cohomology classes (for example, in H3(Emb(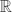 2,
2, 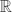 5))) of higher degrees than those of the first nonvanishing homotopy groups.
5))) of higher degrees than those of the first nonvanishing homotopy groups.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 152 , Issue 3 , May 2012 , pp. 497 - 533
- Copyright
- Copyright © Cambridge Philosophical Society 2012
References
REFERENCES
- 2
- Cited by




