Article contents
Hypergraphs with No Cycle of a Given Length
Published online by Cambridge University Press: 02 February 2012
Abstract
Recently, the authors gave upper bounds for the size of 3-uniform hypergraphs avoiding a given odd cycle using the definition of a cycle due to Berge. In the present paper we extend this bound to m-uniform hypergraphs (for all m ≥ 3), as well as m-uniform hypergraphs avoiding a cycle of length 2k. Finally we consider non-uniform hypergraphs 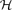 avoiding cycles of length 2k or 2k + 1. In both cases we can bound
avoiding cycles of length 2k or 2k + 1. In both cases we can bound 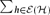 |h| by O(n1+1/k) under the assumption that all h ∈ ε(
|h| by O(n1+1/k) under the assumption that all h ∈ ε(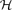 ) satisfy |h| ≥ 4k2.
) satisfy |h| ≥ 4k2.
- Type
- Paper
- Information
- Combinatorics, Probability and Computing , Volume 21 , Issue 1-2: Honouring the Memory of Richard H. Schelp , March 2012 , pp. 193 - 201
- Copyright
- Copyright © Cambridge University Press 2012
References
[1]Bollobás, B. and Győri, E. (2008) Pentagons vs. triangles. Discrete Math. 308 4332–4336.CrossRefGoogle Scholar
[2]Bondy, J. A. and Simonovits, M. (1974) Cycles of even length in graphs. J. Combin. Theory Ser. B 16 97–105.CrossRefGoogle Scholar
[3]Erdős, P. and Gallai, T. (1959) On maximal paths and circuits of graphs. Acta Math. Acad. Sci. Hungar. 10 337–356.CrossRefGoogle Scholar
[4]Gyárfás, A., Jacobson, M., Kézdy, A. and Lehel, J. (2006) Odd cycles and Theta-cycles in hypergraphs. Discrete Math. 306 2481–2491.CrossRefGoogle Scholar
[5]Győri, E. (2006) Triangle-free hypergraphs. Combin. Probab. Comput. 15 185–191.CrossRefGoogle Scholar
[6]Győri, E. and Lemons, N. 3-uniform hypergraphs avoiding a given odd cycle. Combinatorica, to appear.Google Scholar
[7]Kostochka, A. and Verstraete, J. (2005) Even cycles in hypergraphs. J. Combin. Theory Ser. B 94 173–182.CrossRefGoogle Scholar
- 35
- Cited by




