Article contents
Characterization of the flow past a truncated square cylinder in a duct under a spanwise magnetic field
Published online by Cambridge University Press: 05 December 2011
Abstract
We study the flow of an electrically conducting fluid past a truncated square cylinder in a rectangular duct under the influence of an externally applied homogeneous magnetic field oriented along the cylinder axis. Our aim is to bridge the gap between the non-magnetic regime, where we previously found a complex set of three-dimensional recirculations behind the cylinder (Dousset & Pothérat, J. Fluid Mech., vol. 653, 2010, pp. 519–536) and the asymptotic regime of dominating Lorentz force analysed by Hunt & Ludford (J. Fluid. Mech., vol. 33, 1968, pp. 693–714). The latter regime is characterized by a remarkable structure known as Hunt’s wake in the magnetohydrodynamics community, where the flow is deflected on either side of a stagnant zone, right above the truncated cylinder as if the latter would span the full height of the duct. In steady flows dominated by the Lorentz force, with negligible inertia, we provide the first numerical flow visualization of Hunt’s wake. In regimes of finite inertia, a thorough topological analysis of the steady flow regimes reveals how the Lorentz force gradually reorganizes the flow structures in the hydrodynamic wake of the cylinder as the Hartmann number  (which gives a non-dimensional measure of the magnetic field) is increased. The nature of the vortex shedding follows from this rearrangement of the steady structures by the magnetic field. As
(which gives a non-dimensional measure of the magnetic field) is increased. The nature of the vortex shedding follows from this rearrangement of the steady structures by the magnetic field. As 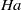 is increased, we observe that the vortex street changes from a strongly symmetric one to the alternate procession of counter-rotating vortices typical of the non-truncated cylinder wakes.
is increased, we observe that the vortex street changes from a strongly symmetric one to the alternate procession of counter-rotating vortices typical of the non-truncated cylinder wakes.
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2011
References
Dousset and Potherat supplementary movie
Animation of the vortex street at $Re=600$ and $Ha=50$: iso-surfaces of $\lambda_2=-20$ for $1212\le t \le1266$. One observes the formation and release of almost symmetric rib-like vortices
Dousset and Potherat supplementary movie
Animation of the vortex street at $Re=600$ and $Ha=50$: iso-surfaces of $\lambda_2=-20$ for $1212\le t \le1266$. One observes the formation and release of almost symmetric rib-like vortices
Dousset and Potherat supplementary movie
Caption: Animation of the vortex street at $Re=800$ and $Ha=100$: iso-surfaces of $\lambda_2=-30$ for $640\le t \le664$. Note the change in the direction along which the vortices are released in the wake
Dousset and Potherat supplementary movie
Caption: Animation of the vortex street at $Re=800$ and $Ha=100$: iso-surfaces of $\lambda_2=-30$ for $640\le t \le664$. Note the change in the direction along which the vortices are released in the wake
- 17
- Cited by




