Article contents
The granular column collapse as a continuum: validity of a two-dimensional Navier–Stokes model with a μ(I)-rheology
Published online by Cambridge University Press: 27 September 2011
Abstract
There is a large amount of experimental and numerical work dealing with dry granular flows (such as sand, glass beads, etc.) that supports the so-called 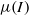 -rheology. The reliability of the
-rheology. The reliability of the 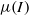 -rheology in the case of complex transient flows is not fully ascertained, however. From this perspective, the granular column collapse experiment provides an interesting benchmark. In this paper we implement the
-rheology in the case of complex transient flows is not fully ascertained, however. From this perspective, the granular column collapse experiment provides an interesting benchmark. In this paper we implement the 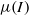 -rheology in a Navier–Stokes solver (Gerris) and compare the resulting solutions with both analytical solutions and two-dimensional contact dynamics discrete simulations. In a first series of simulations, we check the numerical model in the case of a steady infinite two-dimensional granular layer avalanching on an inclined plane. A second layer of Newtonian fluid is then added over the granular layer in order to recover a close approximation of a free-surface condition. Comparisons with analytical and semi-analytical solutions provide conclusive validation of the numerical implementation of the
-rheology in a Navier–Stokes solver (Gerris) and compare the resulting solutions with both analytical solutions and two-dimensional contact dynamics discrete simulations. In a first series of simulations, we check the numerical model in the case of a steady infinite two-dimensional granular layer avalanching on an inclined plane. A second layer of Newtonian fluid is then added over the granular layer in order to recover a close approximation of a free-surface condition. Comparisons with analytical and semi-analytical solutions provide conclusive validation of the numerical implementation of the 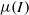 -rheology. In a second part, we simulate the unsteady two-dimensional collapse of granular columns over a wide range of aspect ratios. Systematic comparisons with discrete two-dimensional contact dynamics simulations show good agreement between the two methods for the inner deformations and the time evolution of the shape during most of the flow, while a systematic underestimation of the final run-out is observed. The experimental scalings of spreading of the column as a function of the aspect ratio available from the literature are also recovered. A discussion follows on the performances of other rheologies, and on the sensitivity of the simulations to the parameters of the
-rheology. In a second part, we simulate the unsteady two-dimensional collapse of granular columns over a wide range of aspect ratios. Systematic comparisons with discrete two-dimensional contact dynamics simulations show good agreement between the two methods for the inner deformations and the time evolution of the shape during most of the flow, while a systematic underestimation of the final run-out is observed. The experimental scalings of spreading of the column as a function of the aspect ratio available from the literature are also recovered. A discussion follows on the performances of other rheologies, and on the sensitivity of the simulations to the parameters of the 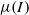 -rheology.
-rheology.
JFM classification
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2011
References
- 268
- Cited by




