Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-17T05:56:07.977Z Has data issue: false hasContentIssue false
  • English
  • Français

The full orbifold K-theory of abelian symplectic quotients

Published online by Cambridge University Press:  10 June 2010

Rebecca Goldin ,
Megumi Harada ,
Tara S. Holm  and
Takashi Kimura
Rebecca Goldin
Affiliation:
Mathematical Sciences MS 3F2, George Mason University, 4400 University Drive, Fairfax, Virginia 22030, USA, rgoldin@math.gmu.edu
Megumi Harada
Affiliation:
Department of Mathematics and Statistics, McMaster University, 1280 Main Street West, Hamilton, Ontario L8S4K1, Canada, Megumi.Harada@math.mcmaster.ca
Tara S. Holm
Affiliation:
Department of Mathematics, 310 Malott Hall, Cornell University, Ithaca, New York 14853-4201, USA, tsh@math.cornell.edu
Takashi Kimura
Affiliation:
Department of Mathematics and Statistics, Boston University, 111 Cummington Street, Boston, Massachusetts 02215, USA, kimura@math.bu.edu
Get access

Abstract

In their 2007 paper, Jarvis, Kaufmann, and Kimura defined the full orbifoldK-theory of an orbifold 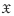, analogous to the Chen-Ruan orbifold cohomology of 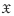in that it uses the obstruction bundle as a quantum correction to the multiplicative structure. We give an explicit algorithm for the computation of this orbifold invariant in the case when 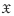arises as an abelian symplectic quotient. To this end, we introduce the inertial K-theory associated to a T -action on a stably complex manifold M, where T is a compact abelian Lie group. Our methods are integral K-theoretic analogues of those used in the orbifold cohomology case by Goldin, Holm, and Knutson in 2005. We rely on the K-theoretic Kirwan surjectivity methods developed by Harada and Landweber. As a worked class of examples, we compute the full orbifold K-theory of weighted projective spaces that occur as a symplectic quotient of a complex affine space by a circle. Our computations hold over the integers, and in the particular case of these weighted projective spaces, we show that the associated invariant is torsion-free.

Keywords

full orbifold K-theoryinertial K-theoryHamiltonian T -spacesymplectic quotient
Type
Research Article
Information
Journal of K-Theory , Volume 8 , Issue 2 , October 2011 , pp. 339 - 362
Copyright
Copyright © ISOPP 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Adem, A. and Ruan, Y.. Twisted orbifold K-theory. Comm. Math. Phys. 237(3):533–556, 2003.Google Scholar
2. Amrani, A. Al. A comparison between cohomology and K-theory of weighted projective spaces. J. Pure App. Alg. 93(2):129–134, 1994.CrossRefGoogle Scholar
3. Amrani, A. Al. Complex K-theory of weighted projective spaces. J. Pure App. Alg. 93(2):113–127, 1994.Google Scholar
4. Amrani, A. Al. Cohomological study of weighted projective spaces. In Algebraic Geometry, Lecture Notes in Pure and Applied Mathematics 193:1–52, 1997.Google Scholar
5. Bahri, A., Franz, M., and Ray, N.. The equivariant cohomology of weighted projective space. Math. Proc. Cambridge Phil. Soc. 146(2):395–405, 2009.Google Scholar
6. Becerra, E. and Uribe, B.. Stringy product on twisted orbifold K-theory for abelian quotients, Trans. Amer. Math. Soc. 361:5781–5803, 2009.Google Scholar
7. Boissiere, S., Mann, E., and Perroni, F.. The cohomological crepant resolution conjecture for ℙ (1,3,4,4). Internat. J. Math. 20(6):791–801, 2009.Google Scholar
8. Borisov, L. A., Chen, L., and Smith, G. G.. The orbifold Chow ring of toric Deligne-Mumford stacks. J. Amer. Math. Soc. 18(1):193–215, 2005.Google Scholar
9. Borisov, L. A. and Horja, R. P.. On the K-theory of smooth toric DM stacks. Contemp. Math. 401:21–42, 2006.CrossRefGoogle Scholar
10. Chen, W. and Ruan, Y.. A new cohomology theory of orbifold. Comm. Math. Phys. 248(1):1–31, 2004.Google Scholar
11. Coates, T., Corti, A., Lee, Y.-P., and Tseng, H.-H.. The quantum orbifold cohomology of weighted projective spaces, Acta Math. 202(2):139–193, 2009.Google Scholar
12. Dixon, L., Harvey, J., Vafa, C., and Witten, E.. Strings on orbifolds. Nuclear Phys. B 261(4): 678–686, 1985.Google Scholar
13. Goldin, R. and Harada, M.. Orbifold cohomology of hypertoric varieties. Internat. J. Math. 19(8): 927–956, 2008.CrossRefGoogle Scholar
14. Goldin, R., Holm, T. S., and Knutson, A.. Orbifold cohomology of torus quotients. Duke Math. J. 139(1):89–139, 2007.CrossRefGoogle Scholar
15. Goresky, M., Kottwitz, R., and MacPherson, R.. Equivariant cohomology, Koszul duality, and the localization theorem. Invent. Math. 131:25–83, 1998.CrossRefGoogle Scholar
16. Guest, M. and Sakai, H.. Orbifold quantum D-modules associated to weighted projective spaces, arXiv:0810.4236.Google Scholar
17. Harada, M., Henriques, A., and Holm, T. S.. Computation of generalized equivariant cohomologies of Kac-Moody flag varieties. Adv. Math. 197(1):198–221, 2005.CrossRefGoogle Scholar
18. Harada, M. and Landweber, G. D.. Surjectivity for Hamiltonian G-spaces in K-theory. Trans. Amer. Math. Soc. 359:6001–6025, 2007.CrossRefGoogle Scholar
19. Harada, M. and Landweber, G. D.. The K-theory of abelian symplectic quotients. Math. Res. Lett. 15(1):57–72, 2008.Google Scholar
20. Holm, T.. Orbifold cohomology of abelian symplectic reductions and the case of weighted projective spaces. Contemp. Math. 450: 127–146, 2008.CrossRefGoogle Scholar
21. Iwanari, I.. The category of toric stacks. Compos. Math. 145(3): 718–746, 2009.CrossRefGoogle Scholar
22. Jarvis, T. J., Kaufmann, R., and Kimura, T.. Stringy K-theory and the Chern character. Invent. Math. 168(1):23–81, 2007.CrossRefGoogle Scholar
23. Jiang, Y. and Tseng, H.-H.. The integral (orbifold) Chow ring of toric Deligne-Mumford stacks, arXiv:math.AG/0707.2972.Google Scholar
24. Kawasaki, T.. Cohomology of twisted projective space and lens complexes. Math. Annalen. 206:243–248, 1973.CrossRefGoogle Scholar
25. Knutson, A.. Weight varieties, MIT Ph.D. thesis, 1996.Google Scholar
26. Lerman, E. and Tolman, S.. Hamiltonian torus actions on symplectic orbifolds and toric varieties. Trans. Amer. Math. Soc. 349(10):4201–4230, 1997.CrossRefGoogle Scholar
27. Nishimura, Y. and Yosimura, Z.. The quasi KO*-types of weighted projective spaces. J. Math. Kyoto Univ. 37(2):251–259, 1997.Google Scholar
28. Segal, G.. Equivariant K-theory. Inst. Hautes Études Sci. Publ. Math. 34:129–151, 1968.CrossRefGoogle Scholar
29. Tolman, S. and Weitsman, J.. The cohomology rings of symplectic quotients. Comm. Anal. Geom. 11(4):751–773, 2003.CrossRefGoogle Scholar
30. Tymoczko, J.. Equivariant structure constants for ordinary and weighted projective space, arXiv:0806.3588.Google Scholar