Article contents
XV.—The Correlation between Relatives on the Supposition of Mendelian Inheritance.
Published online by Cambridge University Press: 06 July 2012
Extract
Several attempts have already been made to interpret the well-established results of biometry in accordance with the Mendelian scheme of inheritance. It is here attempted to ascertain the biometrical properties of a population of a more general type than has hitherto been examined, inheritance in which follows this scheme. It is hoped that in this way it will be possible to make a more exact analysis of the causes of human variability. The great body of available statistics show us that the deviations of a human measurement from its mean follow very closely the Normal Law of Errors, and, therefore, that the variability may be uniformly measured by the standard deviation corresponding to the square root of the mean square error. When there are two independent causes of variability capable of producing in an otherwise uniform population distributions with standard deviations σ1 and σ2, it is found that the distribution, when both causes act together, has a standard deviation 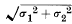 . It is therefore desirable in analysing the causes of variability to deal with the square of the standard deviation as the measure of variability. We shall term this quantity the Variance of the normal population to which it refers, and we may now ascribe to the constituent causes fractions or percentages of the total variance which they together produce. It is desirable on the one hand that the elementary ideas at the basis of the calculus of correlations should be clearly understood, and easily expressed in ordinary language, and on the other that loose phrases about the “percentage of causation,” which obscure the essential distinction between the individual and the population, should be carefully avoided.
. It is therefore desirable in analysing the causes of variability to deal with the square of the standard deviation as the measure of variability. We shall term this quantity the Variance of the normal population to which it refers, and we may now ascribe to the constituent causes fractions or percentages of the total variance which they together produce. It is desirable on the one hand that the elementary ideas at the basis of the calculus of correlations should be clearly understood, and easily expressed in ordinary language, and on the other that loose phrases about the “percentage of causation,” which obscure the essential distinction between the individual and the population, should be carefully avoided.
- Type
- Research Article
- Information
- Earth and Environmental Science Transactions of The Royal Society of Edinburgh , Volume 52 , Issue 2 , 1919 , pp. 399 - 433
- Copyright
- Copyright © Royal Society of Edinburgh 1919
References
page 400 note * The correlation is determined from the measurements of n individuals, x 1, x 2, … x n, and of their brothers, y 1, y 2, …, y r; let us suppose that each pair of brothers is a random sample of two from an infinite fraternity, that is to say from all the sons which a pair of parents might conceivably have produced, and that the variance of each such fraternity is V, while that of the sons in general is σ. Then the mean value of (x–y)2 will be 2V, since each brother contributes the variance V. But expanding the expression, we find the mean value of both x 2 and y 2 is σ2, while that of xy is rσ 2, where r is the fraternal correlation. Hence 2V=2σ2(1−r), or ![]() . Taking the values ·5066 and ·2804 for the parental and marital correlations, we find that the heights of the parents alone account for 40·10 per cent, of the variance of the children, whereas the total effect of ancestry, deduced from the fraternal correlation, is 54·33 per cent.
. Taking the values ·5066 and ·2804 for the parental and marital correlations, we find that the heights of the parents alone account for 40·10 per cent, of the variance of the children, whereas the total effect of ancestry, deduced from the fraternal correlation, is 54·33 per cent.
page 401 note * The case of the fraternal correlations has been unfortunately complicated by the belief that the correlation on a Mendelian hypothesis would depend on the number of the fraternity. In a family, for instance, in which four Mendelian types are liable to occur in equal numbers, it was assumed that of a family of four, one would be of each type; in a family of eight, two of each type; and so on. If this were the case, then in such families, one being of the type A would make it less likely, in small families impossible, for a second to be of this type. If, as was Mendel's hypothesis, the different qualities were carried by different gametes, each brother would havean independent and equal chance of each of the four possibilities. Thus the formulæ giving the fraternal correlations in terms of the number of the fraternity give values too small. The right value on Mendel's theory is that for an infinite fraternity. AS Pearson suggested in the same paper, “probably the most correct way of looking at any fraternal correlation table would be to suppose it a random sample of all pairs of brothers which would be obtained by giving a large, or even indefinitely large, fertility to each pair, for what we actually do is to take families of varying size and take as many pairs of brothers as they provide.” In spite of this, the same confusing supposition appears in a paper by SNOW “On the Determination of the Chief Correlations between Collaterals in the Case of a Simple Mendelian Population Mating at Random” (E. C. SNOW, B.A., Proc. Roy. Soc., June 1910); and in one by Brownlee, John, “The Significance of the Correlation Coefficient when applied to Mendelian Distributions” (Proc. Roy. Soc. Edin., Jan. 1910).CrossRefGoogle Scholar
page 420 note * Pearson, and Lee, , “On the Laws of Inheritance in Man,” Biometrika, ii, 374.Google Scholar
- 2668
- Cited by




