Article contents
On the Lq norm of cyclotomic Littlewood polynomials on the unit circle
Published online by Cambridge University Press: 13 July 2011
Abstract
Let 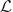 n be the collection of all (Littlewood) polynomials of degree n with coefficients in {−1, 1}. In this paper we prove that if (P2ν) is a sequence of cyclotomic polynomials P2ν ∈
n be the collection of all (Littlewood) polynomials of degree n with coefficients in {−1, 1}. In this paper we prove that if (P2ν) is a sequence of cyclotomic polynomials P2ν ∈ 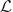 2ν, then
2ν, then
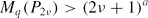 for every q > 2 with some a = a(q) > 1/2 depending only on q, where
for every q > 2 with some a = a(q) > 1/2 depending only on q, where
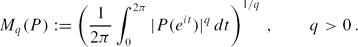 The case q = 4 of the above result is due to P. Borwein, Choi and Ferguson. We also prove that if (P2ν) is a sequence of cyclotomic polynomials P2ν ∈
The case q = 4 of the above result is due to P. Borwein, Choi and Ferguson. We also prove that if (P2ν) is a sequence of cyclotomic polynomials P2ν ∈ 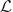 2ν, then
2ν, then
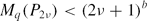 for every 0 < q < 2 with some 0 < b = b(q) < 1/2 depending only on q. Similar results are conjectured for Littlewood polynomials of odd degree. Our main tool here is the Borwein–Choi Factorization Theorem.
for every 0 < q < 2 with some 0 < b = b(q) < 1/2 depending only on q. Similar results are conjectured for Littlewood polynomials of odd degree. Our main tool here is the Borwein–Choi Factorization Theorem.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 151 , Issue 2 , September 2011 , pp. 373 - 384
- Copyright
- Copyright © Cambridge Philosophical Society 2011
References
REFERENCES
- 1
- Cited by




