Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-19T19:13:12.750Z Has data issue: false hasContentIssue false
  • English
  • Français

Fixed points of symplectic periodic flows

Published online by Cambridge University Press:  16 June 2010

ALVARO PELAYO  and
SUSAN TOLMAN
ALVARO PELAYO
Affiliation:
University of California–Berkeley, Mathematics Department, 970 Evans Hall #3840, Berkeley, CA 94720-3840, USA (email: apelayo@math.berkeley.edu)
SUSAN TOLMAN
Affiliation:
UI Urbana-Champaign, Department of Mathematics, 1409 W Green St, Urbana, IL 61801, USA (email: stolman@math.uiuc.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

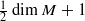The study of fixed points is a classical subject in geometry and dynamics. If the circle acts in a Hamiltonian fashion on a compact symplectic manifold M, then it is classically known that there are at least fixed points; this follows from Morse theory for the momentum map of the action. In this paper we use Atiyah–Bott–Berline–Vergne (ABBV) localization in equivariant cohomology to prove that this conclusion also holds for symplectic circle actions with non-empty fixed sets, as long as the Chern class map is somewhere injective—the Chern class map assigns to a fixed point the sum of the action weights at the point. We complement this result with less sharp lower bounds on the number of fixed points, under no assumptions; from a dynamical systems viewpoint, our results imply that there is no symplectic periodic flow with exactly one or two equilibrium points on a compact manifold of dimension at least eight.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 31 , Issue 4 , August 2011 , pp. 1237 - 1247
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Atiyah, M.. Convexity and commuting Hamiltonians. Bull. Lond. Math. Soc. 14 (1982), 1–15.CrossRefGoogle Scholar
[2]Atiyah, M. and Bott, R.. The moment map and equivariant cohomology. Topology 23 (1984), 1–28.CrossRefGoogle Scholar
[3]Berline, N. and Vergne, M.. Classes caractéristiques équivariantes. Formule de localisation en cohomologie équivariante. C. R. Acad. Sci. Paris 295 (1982), 539–541.Google Scholar
[4]Delzant, T.. Hamiltoniens périodiques et images convexes de l’application moment. Bull. Soc. Math. France 116 (1988), 315–339.CrossRefGoogle Scholar
[5]Duistermaat, J. J. and Pelayo, A.. Symplectic torus actions with coisotropic principal orbits. Ann. Inst. Fourier 57 (2007), 2239–2327.Google Scholar
[6]Godinho, L.. On certain symplectic circle actions. J. Symplectic Geom. 3 (2005), 357–383.CrossRefGoogle Scholar
[7]Guillemin, V. and Sternberg, S.. Convexity properties of the moment mapping. Invent. Math. 67 (1982), 491–513.CrossRefGoogle Scholar
[8]Kirwan, F.. Convexity properties of the moment mapping. III. Invent. Math. 77 (1984), 547–552.CrossRefGoogle Scholar
[9]McDuff, D.. The moment map for circle actions on symplectic manifolds. J. Geom. Phys. 5 (1988), 149–160.CrossRefGoogle Scholar
[10]McDuff, D. and Tolman, S.. Topological properties of Hamiltonian circle actions. Int. Math. Res. Pap. 72826 (2006), 1–77.Google Scholar
[11]Pelayo, A.. Symplectic actions of 2-tori on 4-manifolds. Mem. Amer. Math. Soc. 204(959) (2010), viii+81.Google Scholar
[12]Pelayo, A. and Vũ Ngọc, S.. Semitoric integrable systems on symplectic 4-manifolds. Invent. Math. 177 (2009), 571–597.CrossRefGoogle Scholar
[13]Pelayo, A. and Vũ Ngọc, S.. Constructing integrable systems of semitoric type, Acta Math., arXiv:0903.3376, to appear.Google Scholar
[14]Tolman, S.. On a symplectic generalization of Petrie’s conjecture. Trans. Amer. Math. Soc. 362 (2010), 3963–3996.CrossRefGoogle Scholar
[15]Tolman, S. and Weitsman, J.. On semi-free symplectic circle actions with isolated fixed points. Topology 39 (2000), 299–309.CrossRefGoogle Scholar
[16]Vũ Ngọc, S.. Moment polytopes for symplectic manifolds with monodromy. Adv. Math. 208 (2007), 909–934.CrossRefGoogle Scholar
[17]Weitsman, J.. A Duistermaat–Heckman theorem for symplectic circle actions. Int. Math. Res. Not. (12) (1993), 309–312.CrossRefGoogle Scholar