Article contents
OPTIMAL MIXING OF MARKOV DECISION RULES FOR MDP CONTROL
Published online by Cambridge University Press: 17 May 2011
Abstract
In this article we study Markov decision process (MDP) problems with the restriction that at decision epochs, only a finite number of given Markov decision rules are admissible. For example, the set of admissible Markov decision rules 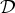 could consist of some easy-implementable decision rules. Additionally, many open-loop control problems can be modeled as an MDP with such a restriction on the admissible decision rules. Within the class of available policies, optimal policies are generally nonstationary and it is difficult to prove that some policy is optimal. We give an example with two admissible decision rules—
could consist of some easy-implementable decision rules. Additionally, many open-loop control problems can be modeled as an MDP with such a restriction on the admissible decision rules. Within the class of available policies, optimal policies are generally nonstationary and it is difficult to prove that some policy is optimal. We give an example with two admissible decision rules—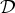 ={d1, d2} —for which we conjecture that the nonstationary periodic Markov policy determined by its period cycle (d1, d1, d2, d1, d2, d1, d2, d1, d2) is optimal. This conjecture is supported by results that we obtain on the structure of optimal
={d1, d2} —for which we conjecture that the nonstationary periodic Markov policy determined by its period cycle (d1, d1, d2, d1, d2, d1, d2, d1, d2) is optimal. This conjecture is supported by results that we obtain on the structure of optimal 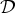 Markov policies in general. We also present some numerical results that give additional confirmation for the conjecture for the particular example we consider.
Markov policies in general. We also present some numerical results that give additional confirmation for the conjecture for the particular example we consider.
- Type
- Research Article
- Information
- Probability in the Engineering and Informational Sciences , Volume 25 , Issue 3 , July 2011 , pp. 307 - 342
- Copyright
- Copyright © Cambridge University Press 2011
References
REFERENCES
- 1
- Cited by




