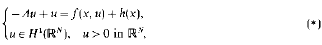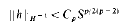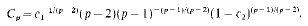Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Deng, Yinbin
and
Li, Yi
2002.
On the Existence of Multiple Positive Solutions for a Semilinear Problem in Exterior Domains.
Journal of Differential Equations,
Vol. 181,
Issue. 1,
p.
197.
Wang, Gengsheng
2002.
Optimal control problems governed by non-well-posed semilinear elliptic equation.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 49,
Issue. 3,
p.
315.
Wang, Hwai-chiuan
2004.
Palais-Smale approaches to semilinear elliptic equations in unbounded domains.
Electronic Journal of Differential Equations,
Vol. 1,
Issue. Mon. 01-09,
p.
06.
Hsu, Tsing-San
and
Lin, Huei-Li
2005.
Bifurcation of positive entire solutions for a semilinear elliptic equation.
Bulletin of the Australian Mathematical Society,
Vol. 72,
Issue. 3,
p.
349.
Bouchekif, Mohammed
and
Nasri, Yasmina
2006.
On a nonhomogeneous elliptic system with changing sign data.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 65,
Issue. 7,
p.
1476.
Wu, Tsung-fang
2006.
Multiplicity and concentration of solutions for nonhomogeneous elliptic equations in multi-bump domains.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 65,
Issue. 10,
p.
1891.
Wu, Tsung-Fang
2006.
On semilinear elliptic equations involving concave–convex nonlinearities and sign-changing weight function.
Journal of Mathematical Analysis and Applications,
Vol. 318,
Issue. 1,
p.
253.
Lin, Huei-Li
2006.
Three positive solutions of semilinear elliptic equations in the half space with a hole.
Journal of Differential Equations,
Vol. 230,
Issue. 2,
p.
614.
Lin, Huei-li
Wang, Hwai-chiuan
and
Wu, Tsung-fang
2007.
Three positive solutions of nonhomogeneous semilinear elliptic equations.
Journal of Mathematical Analysis and Applications,
Vol. 331,
Issue. 2,
p.
1033.
Naito, Yūki
and
Sato, Tokushi
2007.
Positive solutions for semilinear elliptic equations with singular forcing terms.
Journal of Differential Equations,
Vol. 235,
Issue. 2,
p.
439.
Wu, Tsung-Fang
2007.
Existence and Multiplicity of Positive Solutions for Dirichlet Problems in Unbounded Domains.
Abstract and Applied Analysis,
Vol. 2007,
Issue. ,
p.
1.
Hsu, Tsing-San
2007.
Eigenvalue Problems and Bifurcation of Nonhomogeneous Semilinear Elliptic Equations in Exterior Strip Domains.
Boundary Value Problems,
Vol. 2007,
Issue. ,
p.
1.
Chen, Kuan-Ju
and
Peng, Chen-Chang
2007.
Multiplicity and bifurcation of positive solutions for nonhomogeneous semilinear elliptic problems.
Journal of Differential Equations,
Vol. 240,
Issue. 1,
p.
58.
Lin, Huei-Li
Wang, Hwai-Chiuan
and
Wu, Tsung-Fang
2007.
Four positive solutions of semilinear elliptic equations in exterior domains.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 67,
Issue. 4,
p.
1129.
Hsu, Tsing-San
and
Lin, Huei-Li
2007.
Three positive solutions of semilinear elliptic equations in exterior cylinder domains.
Journal of Mathematical Analysis and Applications,
Vol. 332,
Issue. 2,
p.
814.
Wu, Tsung-fang
2009.
Four positive solutions for a semilinear elliptic equation involving concave and convex nonlinearities.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 70,
Issue. 3,
p.
1377.
Wang, Zhengping
and
Zhou, Huan-Song
2009.
Positive solutions for a nonhomogeneous elliptic equation onRNwithout (AR) condition.
Journal of Mathematical Analysis and Applications,
Vol. 353,
Issue. 1,
p.
470.
Hsu, Tsing-san
and
Lin, Huei-li
2010.
Four positive solutions of semilinear elliptic equations involving concave and convex nonlinearities inRN.
Journal of Mathematical Analysis and Applications,
Vol. 365,
Issue. 2,
p.
758.
Hsu, Tsing-san
Lin, Huei-li
and
Hu, Chung-Che
2012.
Multiple positive solutions of quasilinear elliptic equations inRN.
Journal of Mathematical Analysis and Applications,
Vol. 388,
Issue. 1,
p.
500.
Lin, Huei-li
2012.
Positive solutions for nonhomogeneous elliptic equations involving critical Sobolev exponent.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 75,
Issue. 4,
p.
2660.