Article contents
On the initial growth of interfaces in reaction–diffusion equations with strong absorption
Published online by Cambridge University Press: 14 November 2011
Extract
We study the initial growth of the interfaces of non-negative local solutions of the equation ut = (um)xx−λuq when m ≧ 1 and 0<q <1. We show that if 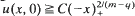 with C < C0, for some explicit C0 = C0(λ, m, q), then the free boundary Ϛ(t) = sup {x:u(x, t) > 0} is a ‘heating front’. More precisely Ϛ(t) ≧at(m−q)/2(1−q) for any t small enough and for some a>0. If on the contrary,
with C < C0, for some explicit C0 = C0(λ, m, q), then the free boundary Ϛ(t) = sup {x:u(x, t) > 0} is a ‘heating front’. More precisely Ϛ(t) ≧at(m−q)/2(1−q) for any t small enough and for some a>0. If on the contrary, 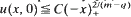 with C<C0, then Ϛ(t) is a ‘cooling front’ and in fact Ϛ(t) ≧ −atm−q)/2(1−q) for any t small enough and for some a > 0. Applications to solutions of the associated Cauchy and Dirichlet problems are also given.
with C<C0, then Ϛ(t) is a ‘cooling front’ and in fact Ϛ(t) ≧ −atm−q)/2(1−q) for any t small enough and for some a > 0. Applications to solutions of the associated Cauchy and Dirichlet problems are also given.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 123 , Issue 5 , 1993 , pp. 803 - 817
- Copyright
- Copyright © Royal Society of Edinburgh 1993
References
- 5
- Cited by




