Article contents
The idempotent generated subsemigroup of the semigroup of continuous endomorphisms of a separable Hilbert space
Published online by Cambridge University Press: 14 November 2011
Extract
Let H be a separable Hilbert space and let CL(H) be the semigroup of continuous, linear maps from H to H. Let E+ be the idempotents of CL(H). Let Ker ɑ and Im ɑ be the null-space and range, respectively, of an element ɑ of CL(H) and let St ɑ be the subspace {x∊H: xɑ = x} of H. It is shown that 〈E+〉 = I∪F∪{i}, where
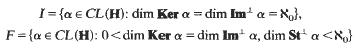
and ι is the identity map. From the proof it is clear that I and F both form subsemigroups of 〈E+〉 and that the depth of I is 3. It is also shown that the depths of F and 〈E+〉 are infinite.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 94 , Issue 3-4 , 1983 , pp. 351 - 360
- Copyright
- Copyright © Royal Society of Edinburgh 1983
References
- 8
- Cited by




