Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Guo, Jong-Shenq
and
Hamel, François
2012.
Propagation and Blocking in Periodically Hostile Environments.
Archive for Rational Mechanics and Analysis,
Vol. 204,
Issue. 3,
p.
945.
Ding, Weiwei
Liang, Xing
and
Xu, Bin
2013.
Spreading speeds of $N$-season spatially periodic integro-difference models.
Discrete and Continuous Dynamical Systems,
Vol. 33,
Issue. 8,
p.
3443.
El Smaily, Mohammad
2013.
The non-monotonicity of the KPP speed with respect to diffusion in the presence of a shear flow.
Proceedings of the American Mathematical Society,
Vol. 141,
Issue. 10,
p.
3553.
Nadin, Gregoire
2015.
How does the spreading speed associated with the Fisher-KPP equation depend on random stationary diffusion and reaction terms?.
Discrete & Continuous Dynamical Systems - B,
Vol. 20,
Issue. 6,
p.
1785.
Bu, Zhen-Hui
and
Wang, Zhi-Cheng
2015.
Curved fronts of monostable reaction-advection-diffusion equations in space-time periodic media.
Communications on Pure and Applied Analysis,
Vol. 15,
Issue. 1,
p.
139.
Wang, Jie
and
Cheng, Cui-Ping
2016.
Spreading speeds and periodic traveling waves of a partially sedentary integro-difference model.
Applied Mathematics and Computation,
Vol. 274,
Issue. ,
p.
459.
Henderson, Christopher
2016.
Propagation of solutions to the Fisher-KPP equation with slowly decaying initial data.
Nonlinearity,
Vol. 29,
Issue. 11,
p.
3215.
Girardin, Léo
2017.
Competition in periodic media:Ⅰ-Existence of pulsating fronts.
Discrete & Continuous Dynamical Systems - B,
Vol. 22,
Issue. 4,
p.
1341.
Girardin, Léo
and
Nadin, Grégoire
2018.
Competition in periodic media: II – Segregative limit of pulsating fronts and “Unity is not Strength”-type result.
Journal of Differential Equations,
Vol. 265,
Issue. 1,
p.
98.
Ito, Ryo
2020.
Determining the optimal coefficient of the spatially periodic Fisher–KPP equation that minimizes the spreading speed.
Journal of Mathematical Biology,
Vol. 80,
Issue. 6,
p.
1953.
Chen, Xinfu
Liang, Xing
and
Tsai, Je-Chiang
2021.
Pulsating waves in a dissipative medium with Delta sources on a periodic lattice.
Journal de Mathématiques Pures et Appliquées,
Vol. 150,
Issue. ,
p.
24.
Liu, Shuang
Lou, Yuan
Peng, Rui
and
Zhou, Maolin
2021.
Asymptotics of the Principal Eigenvalue for a Linear Time-Periodic Parabolic Operator I: Large Advection.
SIAM Journal on Mathematical Analysis,
Vol. 53,
Issue. 5,
p.
5243.
Deng, Liangliang
and
Wang, Zhi-Cheng
2021.
Propagation phenomena for a criss-cross infection model with non-diffusive susceptible population in periodic media.
Discrete & Continuous Dynamical Systems - B,
Vol. 26,
Issue. 9,
p.
4789.
Zhang, Shuo
Feng, Zhaosheng
and
Lin, Guo
2022.
Asymptotic Spreading for a Diffusive Chemostat System in Space-Time Periodic Environment.
Journal of Dynamics and Differential Equations,
Liu, Shuang
Lou, Yuan
and
Song, Pengfei
2022.
A New Monotonicity for Principal Eigenvalues with Applications to Time-Periodic Patch Models.
SIAM Journal on Applied Mathematics,
Vol. 82,
Issue. 2,
p.
576.
Xin, Ming-Zhen
Li, Wan-Tong
and
Bao, Xiongxiong
2023.
Propagation dynamics of nonlocal dispersal monostable equations in time-space periodic habitats.
Journal of Differential Equations,
Vol. 365,
Issue. ,
p.
690.
Lin, Guo
Pan, Shuxia
and
Wang, Xueying
2023.
Spreading Speed of a Cholera Epidemic Model in a Periodic Environment.
Qualitative Theory of Dynamical Systems,
Vol. 22,
Issue. 2,
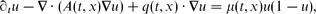 and the spreading speed of the solutions of the Cauchy problem associated with compactly supported initial data. We prove in particular that (1) taking the spatial or temporal average of μ decreases the minimal speed, (2) if μ is not constant with respect to x, then increasing the amplitude of the diffusion matrix A does not necessarily increase the minimal speed and (3) if A = IN, μ is a constant, then the introduction of a space periodic drift term q = ∇Q decreases the minimal speed. In order to prove these results, we use a variational characterisation of the spreading speed that involves a family of periodic principal eigenvalues associated with the linearisation of the equation near zero. We are thus back to the investigation of the dependence relation between this family of eigenvalues and the coefficients.
and the spreading speed of the solutions of the Cauchy problem associated with compactly supported initial data. We prove in particular that (1) taking the spatial or temporal average of μ decreases the minimal speed, (2) if μ is not constant with respect to x, then increasing the amplitude of the diffusion matrix A does not necessarily increase the minimal speed and (3) if A = IN, μ is a constant, then the introduction of a space periodic drift term q = ∇Q decreases the minimal speed. In order to prove these results, we use a variational characterisation of the spreading speed that involves a family of periodic principal eigenvalues associated with the linearisation of the equation near zero. We are thus back to the investigation of the dependence relation between this family of eigenvalues and the coefficients.



