Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Schmincke, U. -W.
1981.
The lower spectrum of Schrödinger operators.
Archive for Rational Mechanics and Analysis,
Vol. 75,
Issue. 2,
p.
147.
Albeverio, S.
Gesztesy, F.
Karwowski, W.
and
Streit, L.
1985.
On the connection between Schrödinger and Dirichlet forms.
Journal of Mathematical Physics,
Vol. 26,
Issue. 10,
p.
2546.
Gesztesy, F.
1986.
Schrödinger Operators, Aarhus 1985.
Vol. 1218,
Issue. ,
p.
93.
Bollé, D.
Gesztesy, F.
Grosse, H.
Schweiger, W.
and
Simon, B.
1987.
Witten index, axial anomaly, and Krein’s spectral shift function in supersymmetric quantum mechanics.
Journal of Mathematical Physics,
Vol. 28,
Issue. 7,
p.
1512.
Gesztesy, F.
1989.
Schrödinger Operators.
Vol. 345,
Issue. ,
p.
93.
Stahlhofen, A.
and
Bleuler, K.
1989.
An algebraic form of the factorization method.
Il Nuovo Cimento B Series 11,
Vol. 104,
Issue. 4,
p.
447.
Stahlhofen, A
1989.
Remarks on the equivalence between the shape-invariance condition and the factorisation condition.
Journal of Physics A: Mathematical and General,
Vol. 22,
Issue. 8,
p.
1053.
Gesztesy, F.
Karwowski, W.
and
Zhao, Z.
1992.
New types of soliton solutions.
Bulletin of the American Mathematical Society,
Vol. 27,
Issue. 2,
p.
266.
Gesztesy, F.
and
Weikard, R.
1993.
Differential Equations with Applications to Mathematical Physics.
Vol. 192,
Issue. ,
p.
101.
Gesztesy, F.
Simon, B.
and
Teschl, G.
1996.
Spectral deformations of one-dimensional Schrödinger operators.
Journal d'Analyse Mathématique,
Vol. 70,
Issue. 1,
p.
267.
Gesztesy, F.
and
Ünal, M.
1998.
Perturbative Oscillation Criteria and Hardy‐Type Ineqalities.
Mathematische Nachrichten,
Vol. 189,
Issue. 1,
p.
121.
Gesztesy, F.
and
Holden, H.
2000.
Darboux-type transformations and hyperelliptic curves.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2000,
Issue. 527,
Spiridonov, V. P.
2001.
Special Functions 2000: Current Perspective and Future Directions.
p.
335.
Schmincke, U.-W.
2003.
On a paper by Gesztesy, Simon, and Teschl concerning isospectral deformations of ordinary Schrödinger operators.
Journal of Mathematical Analysis and Applications,
Vol. 277,
Issue. 1,
p.
51.
Gómez-Ullate, D
Kamran, N
and
Milson, R
2004.
The Darboux transformation and algebraic deformations of shape-invariant potentials.
Journal of Physics A: Mathematical and General,
Vol. 37,
Issue. 5,
p.
1789.
Cascaval, Radu C.
Gesztesy, Fritz
Holden, Helge
and
Latushkin, Yuri
2004.
Spectral analysis of Darboux transformations for the focusing NLS hierarchy.
Journal d'Analyse Mathématique,
Vol. 93,
Issue. 1,
p.
139.
Damanik, David
and
Remling, Christian
2007.
Schrödinger operators with many bound states.
Duke Mathematical Journal,
Vol. 136,
Issue. 1,
Frank, Rupert L.
Simon, Barry
and
Weidl, Timo
2008.
Eigenvalue Bounds for Perturbations of Schrödinger Operators and Jacobi Matrices With Regular Ground States.
Communications in Mathematical Physics,
Vol. 282,
Issue. 1,
p.
199.
Kostenko, Aleksey
Sakhnovich, Alexander
and
Teschl, Gerald
2012.
Commutation methods for Schrödinger operators with strongly singular potentials.
Mathematische Nachrichten,
Vol. 285,
Issue. 4,
p.
392.
Benguria, Rafael D.
2012.
Spectral Analysis of Quantum Hamiltonians.
p.
25.
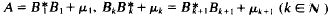 where the μk are suitable numbers which optimally chosen are just the lower eigenvalues of A (if any exist). With the help of this theorem we derive for the special case L0u = −u″ + q(x)u with q(x) → 0 (|x| → ∞) the inequality
where the μk are suitable numbers which optimally chosen are just the lower eigenvalues of A (if any exist). With the help of this theorem we derive for the special case L0u = −u″ + q(x)u with q(x) → 0 (|x| → ∞) the inequality