Article contents
Testing Expansion in Bounded-Degree Graphs
Published online by Cambridge University Press: 09 June 2010
Abstract
We consider the problem of testing expansion in bounded-degree graphs. We focus on the notion of vertex expansion: an α-expander is a graph G = (V, E) in which every subset U ⊆ V of at most |V|/2 vertices has a neighbourhood of size at least α ⋅ |U|. Our main result is that one can distinguish good expanders from graphs that are far from being weak expanders in time 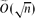 . We prove that the property-testing algorithm proposed by Goldreich and Ron with appropriately set parameters accepts every α-expander with probability at least
. We prove that the property-testing algorithm proposed by Goldreich and Ron with appropriately set parameters accepts every α-expander with probability at least  and rejects every graph that is ϵ-far from any α*-expander with probability at least
and rejects every graph that is ϵ-far from any α*-expander with probability at least  , where
, where 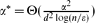 and d is the maximum degree of the graphs. The algorithm assumes the bounded-degree graphs model with adjacency list graph representation and its running time is
and d is the maximum degree of the graphs. The algorithm assumes the bounded-degree graphs model with adjacency list graph representation and its running time is 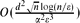 .
.
- Type
- Paper
- Information
- Combinatorics, Probability and Computing , Volume 19 , Issue 5-6: Papers from the 2009 Oberwolfach Meeting on Combinatorics and Probability , November 2010 , pp. 693 - 709
- Copyright
- Copyright © Cambridge University Press 2010
References
- 14
- Cited by




