Nonlinear Schrödinger equations with strongly singular potentials
Published online by Cambridge University Press: 04 August 2010
Abstract
We look for standing waves for nonlinear Schrödinger equations
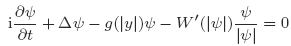
with cylindrically symmetric potentials g vanishing at infinity and non-increasing, and a C1 nonlinear term satisfying weak assumptions. In particular, we show the existence of standing waves with non-vanishing angular momentum with prescribed L2 norm. The solutions are obtained via a minimization argument, and the proof is given for an abstract functional which presents a lack of compactness. As a specific case, we prove the existence of standing waves with non-vanishing angular momentum for the nonlinear hydrogen atom equation.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 140 , Issue 4 , August 2010 , pp. 707 - 721
- Copyright
- Copyright © Royal Society of Edinburgh 2010
- 9
- Cited by




